Testing dynamic correlations and nonlinearity in bivariate time series through information measures and surrogate data analysis

Abstract

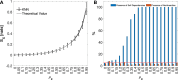
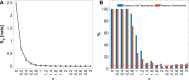
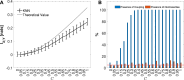
The increasing availability of time series data depicting the evolution of physical system properties has prompted the development of methods focused on extracting insights into the system behavior over time, discerning whether it stems from deterministic or stochastic dynamical systems. Surrogate data testing plays a crucial role in this process by facilitating robust statistical assessments. This ensures that the observed results are not mere occurrences by chance, but genuinely reflect the inherent characteristics of the underlying system. The initial process involves formulating a null hypothesis, which is tested using surrogate data in cases where assumptions about the underlying distributions are absent. A discriminating statistic is then computed for both the original data and each surrogate data set. Significantly deviating values between the original data and the surrogate data ensemble lead to the rejection of the null hypothesis. In this work, we present various surrogate methods designed to assess specific statistical properties in random processes. Specifically, we introduce methods for evaluating the presence of autodependencies and nonlinear dynamics within individual processes, using Information Storage as a discriminating statistic. Additionally, methods are introduced for detecting coupling and nonlinearities in bivariate processes, employing the Mutual Information Rate for this purpose. The surrogate methods introduced are first tested through simulations involving univariate and bivariate processes exhibiting both linear and nonlinear dynamics. Then, they are applied to physiological time series of Heart Period (RR intervals) and respiratory flow (RESP) variability measured during spontaneous and paced breathing. Simulations demonstrated that the proposed methods effectively identify essential dynamical features of stochastic systems. The real data application showed that paced breathing, at low breathing rate, increases the predictability of the individual dynamics of RR and RESP and dampens nonlinearity in their coupled dynamics.

Keywords: complex systems; coupling; information storage; information theory; mutual information rate; surrogate analysis.

FIGURE 1

Schematic description of surrogate frameworks proposed for assessing the presence of self-dependencies and nonlinearities in univariate random processes: (A) presents the Venn diagram of the dependency between the past and the present of the original time series, measured by the IS. In (B), the proposed surrogate procedure to assess the presence of self-dependencies will generate time series where the dependencies between the present and the past are destroyed. In this case, the Venn diagram is presented as two non-intersecting circles. In (C), the surrogate method for detecting nonlinearities will create time series where the nonlinear correlation between the past and the present state of the process is destroyed. Under these conditions, the dependency between the past and the present is not totally destroyed but is equivalent to that arising from a time series with linear correlations only, so the Venn diagram presents a reduced intersection.

FIGURE 2

Schematic description of surrogate frameworks proposed for assessing the presence of coupling, nonlinearities, and temporal correlations in bivariate random processes: (A) presents the Venn diagram of the coupling between two generic processes X (yellow) and Y (blue) measured by MIR, represented in green. In (B), the proposed surrogate procedure to assess the presence of coupling will generate time series where the dependencies between the two processes are destroyed, but dependencies between the past and the present of each process are maintained. In (C), the surrogate method for detecting nonlinearities will create a time series where the nonlinear correlation between the past and the present state of the process is destroyed. For this scenario, the MIR between the processes is not completely lost but is inferior to the original case (A), so the Venn diagram presents a reduced MIR intersection.

FIGURE 3

Distribution of IS KNN estimates, median and 5%–95% percentiles, computed on 100 simulations of a univariate AR model, varying the pole radius ρ _x from 0 to 0.95, is shown in panel (A). In panel (B), the plots depict the percentage of realizations, out of 100 realizations for each value of the pole radius ρ _x , in which the IS was detected as statistically significant (in blue), and for which nonlinearities (in orange) were found. The red line represents the 5% significance level.

FIGURE 4

Distribution of IS KNN estimates, median and 5%–95% percentile range, computed on 100 simulations of Y process defined in Eq. 25, varying the variance noise σ from 0 to 3, is shown in panel (A). In panel (B), the plots depict the percentage of realizations, out of 100 simulation runs for each value of σ, in which the IS was detected as statistically significant (in blue), and for which nonlinearities (in orange) were found. The red line represents the 5% significance level.

FIGURE 5

The distribution of MIR KNN estimates, median, and 5%–95% percentile range, computed on 100 simulations of the VAR process, varying the coupling parameter C from 0 to 1, is shown in black, along with the respective theoretical values in gray, in panel (A). In panel (B), the plots depict the percentage of realizations, out of 100 simulation runs for each value of C, in which the IS MIR detected as statistically significant (in blue), and for which nonlinearities (in orange) were found. The red line represents the 5% significance level.

FIGURE 6

Distribution of MIR KNN estimates, median and 5%–95% percentile range, computed on 100 simulations of Coupled Hénon-Hénon Map, varying the coupling parameter C from 0 to 0.5, is shown in panel (A). In panel (B), the plots depict the percentage of realizations, out of 100 simulation runs for each value of C, in which the IS MIR detected as statistically significant (in blue), and for which nonlinearities (in orange) were found. The red line represents the 5% significance level.

FIGURE 7

Distribution of execution time in msec of (A) surr_ISknn and (B) surr_MIRknn performing only the estimation procedure. The plots present median and 5%–95% percentiles, computed as follows: in (A), based on 100 simulations of a univariate AR model (Eq. 23) with ρ _x =0.5 and f _x =0.3; and in (B), across 100 simulations of the VAR model (Eq. 26) with ρ _x =0.3, f _x =0.3, ρ _y =0.3, f _y =0.1, and C =0.5. For both univariate and bivariate cases, signal lengths N = 100, 500, 1000, 1500, 2000, and embedding dimensions q = 2, 4, 6, 8 were considered.

FIGURE 8

Analysis of the individual dynamics of physiological variability time series. Panels (A, C) display boxplot distributions and individual values of the IS computed on RR and RESP time series, respectively, analyzed during spontaneous breathing (SB) and controlled breathing at 10, 15, and 20 breaths/min (C10, C15, C20). On the right, panels (B, D) present the percentage of individuals exhibiting self-dependencies (blue) and nonlinearities (orange) when considering RR and RESP processes, respectively. Statistical analysis: post hoc test with a Bonferroni correction of the estimated marginal means (EMM) of a repeated measures model:*p < 0.05.

FIGURE 9

Analysis of the coupled dynamics in the cardiorespiratory system S = {RR,RESP}. Panel (A) reports the boxplot distributions and individual values of the MIR, computed during spontaneous breathing (SB) and controlled breathing at 10, 15, and 20 breaths/min (C10, C15, C20). Panel (B) reports the percentage of individuals for which coupling (blue) and nonlinear dynamics (orange) were found. Statistical analysis using a post hoc test with a Bonferroni correction of the estimated marginal means (EMM) of a repeated measures model:*p < 0.05.