Greater cane rat algorithm (GCRA): A nature-inspired metaheuristic for optimization problems

Abstract

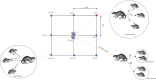
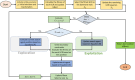
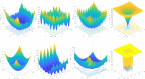
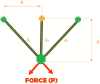
This paper introduces a new metaheuristic technique known as the Greater Cane Rat Algorithm (GCRA) for addressing optimization problems. The optimization process of GCRA is inspired by the intelligent foraging behaviors of greater cane rats during and off mating season. Being highly nocturnal, they are intelligible enough to leave trails as they forage through reeds and grass. Such trails would subsequently lead to food and water sources and shelter. The exploration phase is achieved when they leave the different shelters scattered around their territory to forage and leave trails. It is presumed that the alpha male maintains knowledge about these routes, and as a result, other rats modify their location according to this information. Also, the males are aware of the breeding season and separate themselves from the group. The assumption is that once the group is separated during this season, the foraging activities are concentrated within areas of abundant food sources, which aids the exploitation. Hence, the smart foraging paths and behaviors during the mating season are mathematically represented to realize the design of the GCR algorithm and carry out the optimization tasks. The performance of GCRA is tested using twenty-two classical benchmark functions, ten CEC 2020 complex functions, and the CEC 2011 real-world continuous benchmark problems. To further test the performance of the proposed algorithm, six classic problems in the engineering domain were used. Furthermore, a thorough analysis of computational and convergence results is presented to shed light on the efficacy and stability levels of GCRA. The statistical significance of the results is compared with ten state-of-the-art algorithms using Friedman's and Wilcoxon's signed rank tests. These findings show that GCRA produced optimal or nearly optimal solutions and evaded the trap of local minima, distinguishing it from the rival optimization algorithms employed to tackle similar problems. The GCRA optimizer source code is publicly available at: https://www.mathworks.com/matlabcentral/fileexchange/165241-greater-cane-rat-algorithm-gcra.

Keywords: CEC 2011; CEC 2020; Greater cane rat algorithm; metaheuristic; nature-inspired; optimization; population-based; real-world problem.

Fig. 1

Greater cane rat (image drawn using InkScape version 1.2.1: https://inkscape.org/).

Fig. 2

The natural habitat of the GCR (image drawn using InkScape version 1.2.1: https://inkscape.org/).

Fig. 3

2D possible position vectors (image drawn using InkScape version 1.2.1: https://inkscape.org/).

Fig. 4

Greater cane rats looking for food sources (image drawn using InkScape version 1.2.1: https://inkscape.org/).

Fig. 5

Foraging during mating season (image drawn using InkScape version 1.2.1: https://inkscape.org/).

Fig. 6

The proposed GCRA algorithmic flowchart design.

Fig. 7

2-D representation of characteristics of some classical benchmark function.

Fig. 8

Qualitative results for some of the studied benchmark problems from F1–F13.

Fig. 8

Qualitative results for some of the studied benchmark problems from F1–F13.

Fig. 9

Convergence analysis.

Fig. 10

The 3-BTD.

Fig. 11

The GTD

Fig. 12

The WBD

Fig. 13

The PVD

Fig. 14

The CSD

Fig. 15

The CBD

Fig. 16

Graphical representation of algorithm's performance ranking (algorithm with the least value is ranked higher).