Analysis of fluid force and flow fields during gliding in swimming using smoothed particle hydrodynamics method

Abstract

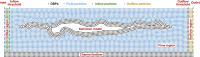
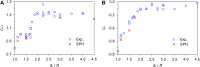
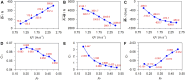
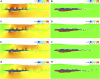
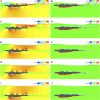
Gliding is a crucial phase in swimming, yet the understanding of fluid force and flow fields during gliding remains incomplete. This study analyzes gliding through Computational Fluid Dynamics simulations. Specifically, a numerical model based on the Smoothed Particle Hydrodynamics (SPH) method for flow-object interactions is established. Fluid motion is governed by continuity, Navier-Stokes, state, and displacement equations. Modified dynamic boundary particles are used to implement solid boundaries, and steady and uniform flows are generated with inflow and outflow conditions. The reliability of the SPH model is validated by replicating a documented laboratory experiment on a circular cylinder advancing steadily beneath a free surface. Reasonable agreement is observed between the numerical and experimental drag force and lift force. After the validation, the SPH model is employed to analyze the passive drag, vertical force, and pitching moment acting on a streamlined gliding 2D swimmer model as well as the surrounding velocity and vorticity fields, spanning gliding velocities from 1 m/s to 2.5 m/s, submergence depths from 0.2 m to 1 m, and attack angles from -10° to 10°. The results indicate that with the increasing gliding velocity, passive drag and pitching moment increase whereas vertical force decreases. The wake flow and free surface demonstrate signs of instability. Conversely, as the submergence depth increases, there is a decrease in passive drag and pitching moment, accompanied by an increase in vertical force. The undulation of the free surface and its interference in flow fields diminish. With the increase in the attack angle, passive drag and vertical force decrease whereas pitching moment increases, along with the alteration in wake direction and the increasing complexity of the free surface. These outcomes offer valuable insights into gliding dynamics, furnishing swimmers with a scientific basis for selecting appropriate submergence depth and attack angle.

Keywords: flow field; fluid force; gliding; numerical analysis; smoothed particle hydrodynamics (SPH); swimming.

FIGURE 1

Simplified 2D swimmer model with a streamlined prone posture.

FIGURE 2

Illustration of the boundary conditions of the SPH model.

FIGURE 3

Sketch of the numerical setup of a circular cylinder advancing steadily beneath a free surface.

FIGURE 4

Sketch of the numerical setup of gliding in swimming.

FIGURE 5

Comparison between the numerical and experimental fluid force coefficients. (A) Drag coefficient. (B) Lift coefficient.

FIGURE 6

Fluid force and corresponding coefficients under various gliding velocities. (A) Passive drag. (B) Vertical force. (C) Pitching moment. (D) Drag coefficient. (E) Vertical coefficient. (F) Pitching coefficient.

FIGURE 7

Velocity and vorticity fields under various gliding velocities. (A) Velocity field under U = 1.0 m/s. (B) Vorticity field under U = 1.0 m/s. (C) Velocity field under U = 1.5 m/s. (D) Vorticity field under U = 1.5 m/s. (E) Velocity field under U = 2.0 m/s. (F) Vorticity field under U = 2.0 m/s. (G) Velocity field under U = 2.5 m/s. (H) Vorticity field under U = 2.5 m/s.

FIGURE 8

Fluid force under various submergence depths. (A) Passive drag. (B) Vertical force. (C) Pitching moment.

FIGURE 9

Velocity and vorticity fields under various submergence depths. (A) Velocity field under d _s = 0.2 m. (B) Vorticity field under d _s = 0.2 m. (C) Velocity field under d _s = 0.4 m. (D) Vorticity field under d _s = 0.4 m. (E) Velocity field under d _s = 0.6 m. (F) Vorticity field under d _s = 0.6 m. (G) Velocity field under d _s = 0.8 m. (H) Vorticity field under d _s = 0.8 m. (I) Velocity field under d _s = 1.0 m. (J) Vorticity field under d _s = 1.0 m.

FIGURE 10

Fluid force under various attack angles. (A) Passive drag. (B) Vertical force. (C) Pitching moment.

FIGURE 11

Velocity and vorticity fields under various attack angles. (A) Velocity field under θ = −10°. (B) Vorticity field under θ = −10°. (C) Velocity field under θ = −5°. (D) Vorticity field under θ = −5°. (E) Velocity field under θ = 0. (F) Vorticity field under θ = 0. (G) Velocity field under θ = 5°. (H) Vorticity field under θ = 5°. (I) Velocity field under θ = 10°. (J) Vorticity field under θ = 10°.