Modeling dynamics of acute HIV infection incorporating density-dependent cell death and multiplicity of infection

Abstract

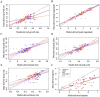
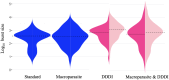
Understanding the dynamics of acute HIV infection can offer valuable insights into the early stages of viral behavior, potentially helping uncover various aspects of HIV pathogenesis. The standard viral dynamics model explains HIV viral dynamics during acute infection reasonably well. However, the model makes simplifying assumptions, neglecting some aspects of HIV infection. For instance, in the standard model, target cells are infected by a single HIV virion. Yet, cellular multiplicity of infection (MOI) may have considerable effects in pathogenesis and viral evolution. Further, when using the standard model, we take constant infected cell death rates, simplifying the dynamic immune responses. Here, we use four models-1) the standard viral dynamics model, 2) an alternate model incorporating cellular MOI, 3) a model assuming density-dependent death rate of infected cells and 4) a model combining (2) and (3)-to investigate acute infection dynamics in 43 people living with HIV very early after HIV exposure. We find that all models qualitatively describe the data, but none of the tested models is by itself the best to capture different kinds of heterogeneity. Instead, different models describe differing features of the dynamics more accurately. For example, while the standard viral dynamics model may be the most parsimonious across study participants by the corrected Akaike Information Criterion (AICc), we find that viral peaks are better explained by a model allowing for cellular MOI, using a linear regression analysis as analyzed by R2. These results suggest that heterogeneity in within-host viral dynamics cannot be captured by a single model. Depending on the specific aspect of interest, a corresponding model should be employed.

Fig 1. Viral load measurements from the RV217 study participants.

Viral load measurements from A) all 77 participants from the RV217 study, B) the 43 study participants that were included in our analysis and C) from 34 study participants excluded from our analysis (grey lines) along with representative viral load trajectories (colored lines).

Fig 2. Viral quantitative measurements estimation and summary statistics.

A) Example of how quantitative measures are estimated for each study participant. Points represent viral load measurements. Red points were identified as part of the growth phase and were used to estimate the growth rate via linear regression (red line). Similarly, the orange and blue points were identified as part of the viral decay phase and setpoint, respectively, and are graphed with regression lines. B) Summary statistics of quantitative measurements for the 43 study participants included in our analysis. Peak magnitude refers to the peak viremia predicted by the intersection of the growth and decay lines and peak time, the time when the viral peak occurs. We also derive a metric for the overal characterization the peak, called peak joint and defined as $\frac{\text{peak}\text{magnitude-mean}\text{peak}\text{magnitude}}{\text{mean}\text{peak}\text{magnitude}}+\frac{\text{peak}\text{timing-mean}\text{peak}\text{timing}}{\text{mean}\text{peak}\text{timing}}$.

Fig 3. Standard viral dynamics model and Macroparasite model.

A) Schematic of the standard model. Target cells, T are sourced at rate s and die at rate d. Virus V infects target cells at rate β. Infected cells, I die at rate δ and produce virions at rate p. Free virus gets cleared at rate c. B) Schematic of the Macroparasite model. Target cells, H_i are produced at a constant rate a and die at rate b. Target cells can be uninfected or infected with i virions. Here we demonstrate cells infected with up to 2 virions. Free virus infects target cells at rate β. Virus-induced mortality of infected cells is α_i. Infected cells produce free virus at rate λ_i. Virus gets cleared at rate η. In these schematics, c and η represent the same parameter, viral clearance. We choose to keep them separate to avoid confusion and remain consistent with previous publications.

Fig 4. Model fits to study participant viral loads.

Viral load measurements for four representative study participant (black points) and fitted curves for the Standard model (blue line), Density dependent death of infected cells(DDDI) model (cyan line), MOI model (red line) and Density dependent cell death model & MOI model (orange line). There are study participants where all models are comparably good at capturing the viral load data (A and B), whereas others (C) where they do not. We also show a case where the MOI model is better able to capture the viral peak (D).

Fig 5. Estimated burst size distributions.

Violin plots of the estimated viral burst sizes (on the $\mathrm{l}o{g}_{10}$ scale) along with the median estimates (black dashed lines) for the all models. For the Standard and Macroparasite models, burst size remains constant throughout the course of acute infection (blue violins). For the models incorporating density-dependence in the death of infected cells DDDI, burst size changes over time and here we report the minimum (pink half-violin) and maximum estimates (soft pink half-violin). Details of the burst size calculations are included in the S2 Text.

Fig 6. Regressions for all viral quantitative measures.

Data-derived and model-derived quantitative measurements (solid points) for each study participant and model, along with the fitted linear regression lines (solid lines) for the growth rate (A), peak magnitude (B), decay rate (C), peak time (D), joint peak measurement(E) and setpoint (F). The model that explains best a quantitative measurement is the one where the model-derived value is closest to the data-derived value, i.e the fitted linear regression is closest to the y = x line (dashed line). Statistical summaries of the fitted regressions can be found in Table 3.