Prokrustean Graph: A substring index for rapid k-mer size analysis

Abstract

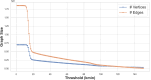
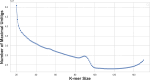
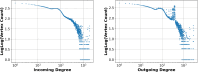
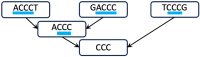
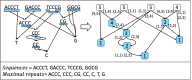
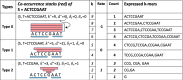
The widespread adoption of k-mers in bioinformatics has led to efficient methods utilizing genomic sequences in a variety of biological tasks. However, understanding the influence of k-mer sizes within these methods remains a persistent challenge, as the outputs of complex bioinformatics pipelines obscure this influence with various noisy factors. The choice of k-mer size is often arbitrary, with justification frequently omitted in the literature and method tutorials. Furthermore, recent methods employing multiple k-mer sizes encounter significant computational challenges. Nevertheless, most methods are built on well-defined objects related to k-mers, such as de Bruijn graphs, Jaccard similarity, Bray-Curtis dissimilarity, and k-mer spectra. The role of k-mer sizes within these objects is more intuitive and can be described by numerous quantities and metrics. Therefore, exploring these objects across k-mer sizes opens opportunities for robust analyses and new applications. However, the evolution of k-mer objects with respect to k-mer sizes is surprisingly elusive. We introduce a novel substring index, the Prokrustean graph, that elucidates the transformation of k-mer sets across k-mer sizes. Our framework built upon this index rapidly computes k-mer-based quantities for all k-mer sizes, with computational complexity independent of the size range and dependent only on maximal repeats. For example, counting maximal simple paths in de Bruijn graphs for $k=1,\dots ,100$ is achieved in seconds using our index on a gigabase-scale dataset. We present a variety of such experiments relevant to pangenomics and metagenomics. The Prokrustean graph is space-efficiently constructed from the Burrows-Wheeler Transform. Through this construction, it becomes evident that other modern substring indices inherently face difficulties in exploring k-mer objects across sizes, which motivated our data structure. Our implementation is available at: https://github.com/KoslickiLab/prokrustean.

Fig.1:

Size decay of a Prokrustean graph as a function of $k_{min}$. The sizes of Prokrustean graphs, i.e., number of vertices and edges, versus $k_{min}$ values for a short read dataset ERR3450203 are depicted. The size of the graph rapidly drops around $k_{min}=[11,\dots ,19]$, meaning the maximal repeats and locally-maximal repeat regions are dense when $k_{min}$ is under 11. The number of edges falls again around $k_{min}=100$ because the graph eventually becomes fully disconnected.

Fig.2:

The number of maximal unitigs in de Bruijn graphs of order k = 20,...,150 of metagenomic short reads (ERR3450203). A complex scenario is revealed: The decrease of the numbers fluctuates in k = 30,...,60, and the peak around k = 90 corresponds to the sudden decrease in maximal repeats. Lastly, further disconnections increase contigs and eventually make the graph completely disconnected.

Fig.3:

Bray-Curtis dissimilarities between four metagenomic samples computed with Algorithm S2. We used the sequencing data of four samples derived from infant fecal microbiota, which were studied in [36]. Samples include two from 12-month-old human subjects and two from 3-week-olds. The relative order between values shift as k changes, e.g. compared to all other dissimilarities, the dissimilarity between sample 2 and 4 is highest at k = 8 but lowest at k = 21. Note that diverse k sizes (10, 12, 21, 31) are actively utilized in practice.

Fig.4:

Vertex degrees of the overlap graph of metagenomic short reads (ERR3450203) computed with Algorithm S4. The number of vertices per each degree is scaled as log log y. There is a clear peak around 10² at both incoming and outgoing degrees, which may imply dense existence of abundant species. The intermittent peaks after 10² might be related to repeating regions within and across species.

Fig.5:

Recursive repeats. At each sequence on the top level, locally-maximal repeat regions (indicated with blue underlining) are used to denote substrings that are more frequent than its superstring. The arrows then points to a node of the substring, and the process can repeat hierarchically.

Fig.6:

The Prokrustean graph of $\mathcal{U}=\left\{\text{ACCCT,GACCC,TCCCG,GGCG}\right\}$. The left graph illustrates the recursion of locally-maximal repeat regions, depicted as blue regions, following the same rule described in Figure 5. The Prokrustean graph on the right represents the same structure that white vertices correspond to sequences $\left(\mathcal{U}\right)$ and blue vertices represent maximal repeats $\left({\mathcal{R}}_{\mathcal{U}}\right)$ found through the recursion process shown in the left graph. The strings are not stored, so integer labels store the regions and the size of the substrings.

Fig.7:

Complementary regions. Blue underlining depicts locally maximal regions, and red underlining depicts regions that complement k-mers not covered in blue regions, given k values of 3 and 4. Every k-mer appears exactly once within a red region. For example, in the left image, the 3-mer ACC is included in a red region within ACCCC and does not appear again in any other red region. Note that red regions can include multiple co-occurring k-mers. So, in the right image, both 4-mers TCCC and CCCG co-occur within TCCCG.

Fig.8:

Three types of maximal co-occurrence stacks. Maximal co-occurrence stacks of $S$ (sets of red rectangles) are introduced at each row for each type, given two locally-maximal repeat regions in $S$ (blue rectangles). The Rate column describes the change in the count of expressed k-mers as the k-mer size increases by 1. Hence, the rate is ${\delta }_l+{\delta }_r-1$. Also, ${\delta }_l$ and ${\delta }_r$ control the vertical shapes of stacks. For example, the Type 0 stack forms like a rectangle with ${\delta }_l={\delta }_r=0$, but the Type 1 stack forms like stairs on its left with ${\delta }_l=1$.