A spatial approach to jointly estimate Wright's neighborhood size and long-term effective population size

Abstract

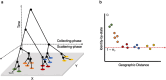
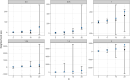
Spatially continuous patterns of genetic differentiation, which are common in nature, are often poorly described by existing population genetic theory or methods that assume either panmixia or discrete, clearly definable populations. There is therefore a need for statistical approaches in population genetics that can accommodate continuous geographic structure, and that ideally use georeferenced individuals as the unit of analysis, rather than populations or subpopulations. In addition, researchers are often interested in describing the diversity of a population distributed continuously in space; this diversity is intimately linked to both the dispersal potential and the population density of the organism. A statistical model that leverages information from patterns of isolation by distance to jointly infer parameters that control local demography (such as Wright's neighborhood size), and the long-term effective size (Ne) of a population would be useful. Here, we introduce such a model that uses individual-level pairwise genetic and geographic distances to infer Wright's neighborhood size and long-term Ne. We demonstrate the utility of our model by applying it to complex, forward-time demographic simulations as well as an empirical dataset of the two-form bumblebee (Bombus bifarius). The model performed well on simulated data relative to alternative approaches and produced reasonable empirical results given the natural history of bumblebees. The resulting inferences provide important insights into the population genetic dynamics of spatially structured populations.

Keywords: Bayesian; continuous space; effective population size; isolation by distance; spatial population genetics.

Fig. 1.

Relationship between the separation-of-timescales of the coalescent and the isolation-by-distance curve in continuous space. a) A single representative gene tree showing the relationships between sampled individuals (colored circles) across a continuous landscape with dimensionality (x, y). Relative to a focal sample (dotted circle), the transition to the collecting phase occurs as the rate of coalescence converges to a neutral Kingman's coalescence. b) An isolation-by-distance plot relative to the focal individual. The transition to the collecting phase occurs when geographic distance is no longer predictive of genetic distance (i.e. pairwise heterozygosity). The red dotted line denotes s (or 1 – π_c), which is the estimated mean minimum relatedness between individuals in the population.

Fig. 2.

Expected relatedness decay curves of ${\mathrm{\Omega }}_{i,j}$ with distance given s = 0.95 for various values of $\mathcal{N}$ (Equation 5 in the text).

Fig. 3.

Model accuracy and precision. a) Estimates of Wright's neighborhood size for each value of K and σ (gray header); black circles are medians and error bars are the 95% quantile. Blue circles are the theoretical $\mathcal{N}$. b) As in (a), but for estimates of π_c. Blue circles represent π when d_ij > 20.

Fig. 4.

Results of Rousset's method for estimating $\mathcal{N}$ across datasets simulated with different values of K (population density in SLiM; x-axis) and σ (dispersal; gray header). As in Fig. 3a, black dots and bars are the estimated values with the median and 95% quantile; blue dots are the true $\mathcal{N}$ for each simulation. Notice the axes differ greatly between Fig. 3a and this figure, demonstrating the wide variance in Rousset's estimator. Supplementary Figs. 15–17 show Rousset's estimator conditioned by various maximum distance thresholds.

Fig. 5.

Empirical application of the method. a) Sample sites of B. bifarius from Jackson et al. (2018a), size of circles represent the number of individuals sampled, and dark gray shading is the known range extent. b) Density of $\mathcal{N}$ estimates across all five chains. c) Density of N_e estimates, where N_e = ${\hat{\pi }}_c/4\mu$, and μ is the empirically estimated mutation rate for bumblebees (Liu et al. 2017).