Prior frequency guided diffusion model for limited angle (LA)-CBCT reconstruction

Abstract

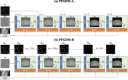
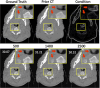
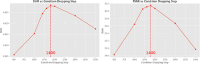
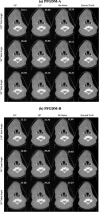
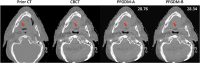
Objective.Cone-beam computed tomography (CBCT) is widely used in image-guided radiotherapy. Reconstructing CBCTs from limited-angle acquisitions (LA-CBCT) is highly desired for improved imaging efficiency, dose reduction, and better mechanical clearance. LA-CBCT reconstruction, however, suffers from severe under-sampling artifacts, making it a highly ill-posed inverse problem. Diffusion models can generate data/images by reversing a data-noising process through learned data distributions; and can be incorporated as a denoiser/regularizer in LA-CBCT reconstruction. In this study, we developed a diffusion model-based framework, prior frequency-guided diffusion model (PFGDM), for robust and structure-preserving LA-CBCT reconstruction.Approach.PFGDM uses a conditioned diffusion model as a regularizer for LA-CBCT reconstruction, and the condition is based on high-frequency information extracted from patient-specific prior CT scans which provides a strong anatomical prior for LA-CBCT reconstruction. Specifically, we developed two variants of PFGDM (PFGDM-A and PFGDM-B) with different conditioning schemes. PFGDM-A applies the high-frequency CT information condition until a pre-optimized iteration step, and drops it afterwards to enable both similar and differing CT/CBCT anatomies to be reconstructed. PFGDM-B, on the other hand, continuously applies the prior CT information condition in every reconstruction step, while with a decaying mechanism, to gradually phase out the reconstruction guidance from the prior CT scans. The two variants of PFGDM were tested and compared with current available LA-CBCT reconstruction solutions, via metrics including peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM).Main results.PFGDM outperformed all traditional and diffusion model-based methods. The mean(s.d.) PSNR/SSIM were 27.97(3.10)/0.949(0.027), 26.63(2.79)/0.937(0.029), and 23.81(2.25)/0.896(0.036) for PFGDM-A, and 28.20(1.28)/0.954(0.011), 26.68(1.04)/0.941(0.014), and 23.72(1.19)/0.894(0.034) for PFGDM-B, based on 120°, 90°, and 30° orthogonal-view scan angles respectively. In contrast, the PSNR/SSIM was 19.61(2.47)/0.807(0.048) for 30° for DiffusionMBIR, a diffusion-based method without prior CT conditioning.Significance. PFGDM reconstructs high-quality LA-CBCTs under very-limited gantry angles, allowing faster and more flexible CBCT scans with dose reductions.

Keywords: cone-beam CT; diffusion model; image reconstruction; limited angle.

Figure 1.

Overview of the two PFGDM variants: PFGDM-A and PFGDM-B. Starting from the Gaussian noise ${\mathit{x}}_T$, in each SDE step of the diffusion model (blue box), we sample a LA-CBCT image ${\mathit{x}}_t^{\prime }$ from the posterior by applying the reverse diffusion that is conditioned on the high-frequency prior CT information. Concurrent with the diffusion model, the LA-CBCT image is also iteratively updated via ADMM based on the given LA-CBCT sinogram (orange box), until convergence. (a) For PFGDM-A, the conditional input $H_{\eta }$ remains unchanged during reconstruction and is dropped after ${\mathit{x}}_{t_d-1}$. (b) For PFGDM-B, the conditional input $H_{{\eta }_t}$ is continuously introduced along the process while dynamically updated to gradually phase out the edge information of the prior CT.

Figure 2.

Samples from the head and neck dataset: the prior CT scan (left), the extracted high-frequency information of the prior CT scan (middle), and the CBCT scan (right) of the same patient.

Figure 3.

Comparison between reconstructed LA-CBCTs, with the high-frequency prior CT condition dropped at different iteration steps (500, 1400, and 2500) for PFGDM-A. The reconstructions are based on an orthogonal-view 90° scan angle (45° for each view), using a total of 3000 iteration steps. PSNR scores measured against the ‘ground-truth’ fully-sampled CBCT are indicated at the top-left corner.

Figure 4.

Variations of the LA-CBCT reconstruction quality/accuracy given different condition-dropping steps for PFGDM-A on the test set, with a total reconstruction step of 3000. The limited-angle projections were simulated with orthogonal-view acquisitions for a total scan angle of ${30}^{\circ }\left(\left[0^{\circ },{15}^{\circ }\right],\left[{90}^{\circ },{105}^{\circ }\right]\right),{90}^{\circ }\left(\left[0^{\circ },{45}^{\circ }\right],\left[{90}^{\circ },{135}^{\circ }\right]\right)$, or ${120}^{\circ }\left(\left[0^{\circ },{60}^{\circ }\right],\left[{90}^{\circ },{150}^{\circ }\right]\right)$.

Figure 5.

Visual comparison between the reconstructed LA-CBCTs of different methods and the ‘ground truth’. In subfigure (a), first, third, and fifth rows represent axial, coronal, and sagittal views, respectively, and the second, fourth, and sixth rows show a zoomed-in region of the corresponding views. In subfigures (b) and (c), first, third, and fourth rows represent axial, coronal, and sagittal views, respectively, and the second row shows a zoomed-in region of the axial view. The limited-angle projections were simulated with either orthogonal-view (ortho) acquisitions for a total scan angle of ${30}^{\circ }\left(\left[0^{\circ },{15}^{\circ }\right],\left[{90}^{\circ },{105}^{\circ }\right]\right),{90}^{\circ }\left(\left[0^{\circ },{45}^{\circ }\right],\left[{90}^{\circ },{135}^{\circ }\right]\right)$, or ${120}^{\circ }\left(\left[0^{\circ },{60}^{\circ }\right],\left[{90}^{\circ },{150}^{\circ }\right]\right);$ or single-view (single) acquisitions for a total scan angle of ${30}^{\circ }\left(\left[0^{\circ },{30}^{\circ }\right]\right),{90}^{\circ }\left(\left[0^{\circ },{90}^{\circ }\right]\right),$ or ${120}^{\circ }\left(\left[0^{\circ },{120}^{\circ }\right]\right)$. Three scenarios of different total scan angles and anatomies are shown as panel (a)–(c) respectively. PSNR scores of each reconstruction on axial slices against the ‘ground truth’ are indicated at the top-right corner of each figure. See table 1 for quantitative results.

Figure 6.

Performance of PFGDM-A and PFGDM-B under extremely limited scan angle scenarios. The limited-angle projections were simulated with orthogonal-view acquisitions for a total scan angle of 2, 8 or 10. PSNR scores of each reconstruction against the ‘ground truth’ are indicated at the top-left corner of each figure. See table 2 for quantitative results.

Figure 7.

Performance of PFGDM-A and PFGDM-B under noise-augmented projections. 10⁵ and 10⁶ indicate the photon number per pixel used for noise simulation, with a smaller photon number corresponding to a higher noise level. The limited-angle projections were simulated with either orthogonal-view (ortho) acquisitions for a total scan angle of 30°([0°,15°],[90°,105°]), 90°([0°,45°],[90°,135°]), or 120°([0°,60°],[90°,150°]). PSNR scores of each reconstruction against the ‘ground truth’ are indicated at the top-right corner of each figure. See table 3 for quantitative results.

Figure 8.

Performance of PFGDM-A and PFGDM-B under scenarios of prior frequency guidance misaligned with the ‘ground-truth’ CBCT. 1 mm, 2 mm, and 4 mm indicate the misalignment magnitudes. The limited-angle projections were simulated with either orthogonal-view (ortho) acquisitions for a total scan angle of 30°([0°,15°],[90°,105°]), 90°([0°,45°],[90°,135°]), or 120°([0°,60°],[90°,150°]). PSNR scores of each reconstruction against the ‘ground truth’ are indicated at the top-right corner of each figure. See table 4 for quantitative results.

Figure 9.

Visual comparisons of the reconstructed LA-CBCTs between PFGDM-A with no prior information (condition dropping step equals to 1), PFGDM-A with a condition dropping step of 1400, PFGDM-B, and the ‘ground-truth’ CBCT. The limited-angle projections were simulated with either orthogonal-view (ortho) acquisitions for a total scan angle of 30°([0°,15°],[90°,105°]), 90°([0°,45°],[90°,135°]), or 120°([0°,60°],[90°,150°]). PSNR scores of each reconstruction on axial slices against the ‘ground truth’ are indicated at the top-right corner of each figure. See table 5 for quantitative results.

Figure 10.

Visual results on the reconstructed LA-CBCTs by removing the ADMM step. The limited-angle projections were simulated with orthogonal-view acquisitions for a total scan angle of ${90}^{\circ }\left(\left[0^{\circ },{45}^{\circ }\right],\left[{90}^{\circ },{135}^{\circ }\right]\right)$. PSNR scores of each reconstruction on axial slices against the ‘ground truth’ are indicated at the top-right corner of each figure. See table 5 for quantitative results.

Figure 11.

Sample conditional input of PFGDM-B from reconstruction step 0 to step 3000, with a step-interval of 500.

Figure 12.

PFGDM-A and PFGDM-B reconstruction results when CT/CBCT have clear anatomical differences. The limited-angle projections were simulated by the orthogonal-view geometry for a total scan angle of ${120}^{\circ }\left(\left[0^{\circ },{60}^{\circ }\right],\left[{90}^{\circ },{150}^{\circ }\right]\right)$. PSNR scores of each reconstruction against the ‘ground-truth’ CBCT are indicated at the top-right corner.