Using random forests to uncover the predictive power of distance-varying cell interactions in tumor microenvironments

Abstract

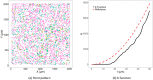
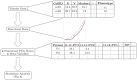
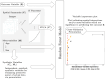
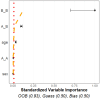
Tumor microenvironments (TMEs) contain vast amounts of information on patient's cancer through their cellular composition and the spatial distribution of tumor cells and immune cell populations. Exploring variations in TMEs between patient groups, as well as determining the extent to which this information can predict outcomes such as patient survival or treatment success with emerging immunotherapies, is of great interest. Moreover, in the face of a large number of cell interactions to consider, we often wish to identify specific interactions that are useful in making such predictions. We present an approach to achieve these goals based on summarizing spatial relationships in the TME using spatial K functions, and then applying functional data analysis and random forest models to both predict outcomes of interest and identify important spatial relationships. This approach is shown to be effective in simulation experiments at both identifying important spatial interactions while also controlling the false discovery rate. We further used the proposed approach to interrogate two real data sets of Multiplexed Ion Beam Images of TMEs in triple negative breast cancer and lung cancer patients. The methods proposed are publicly available in a companion R package funkycells.

Fig 1. An example of point pattern data and an associated K function.

(a) Point pattern data associated with a tumor imaged using MIBIscope from a triple negative breast cancer patient with multiple identified phenotypes. The x- and y-axes represent the spatial dimensions, with the points giving individual cell locations, and the colour of the points indicating one of 15 unique phenotypes, e.g. tumor (red), NK cells (purple), and monocytes/neutrophils (cyan). (b) The associated cross K function (black) for two cell types in the image: tumor and monocytes/neutrophils. The x-axis indicates the radius, r, and the y-axis gives the value of the K function. The estimated K function can be compared to πr² (red dashed line), which is the theoretical K function associated with complete spatial randomness.

Fig 2. Flow chart for data processing.

The methods presented here begin with tabular data obtained after pre-processing multiplex images (steps that include cell segmentation, phenotyping, etc.). For a given image the tabular data consists of rows for each imaged cell, giving the associated x-y position, marker intensities, and cell phenotype. Next, the tabular data are converted into spatial K functions for each interaction of interest (this can be exhaustive, and include all possible interactions between phenotypes, or selective, with only a subset of interactions analysed). Next, K functions are converted into functional principal component scores. Patient meta-variables are added at this stage. The resulting data is then used in the statistical model, as described in Fig 3.

Fig 3. Flow chart of model.

When modeling using funkycells, there are several major steps: organizing data, generating synthetic data, and modeling using random forests. The spatial data is organized into functional summaries (K functions) that are projected into finite dimensions (FPCA) and used with meta-variables to predict the outcome variable. The spatial data and meta-variables are permuted to create synthetic variables with similar properties but independent of the outcome. These synthetic variables are then added to the model, and used to quantify the strength of the relationships between the spatial and meta-data with the response. The model processes the data, employing cross-validation and permutation to return a variable importance plot (with predictive accuracy estimates) indicating spatial interactions and/or meta-variables which are significant in predicting the outcome Z.

Fig 4. Sample variance importance plot.

This sample variable importance plot uses simulated data with a binary outcome, two cell types, and two meta-variables. The data was simulated with significant differences between the outcomes in the B_B, A_B spatial interactions, and age meta-variable, but no significant difference across sex and the A_A spatial interaction. The point estimates of the variable importance values are the black dots, with accompanying intervals indicating the uncertainty. The red dotted straight line is the noise threshold and the orange dashed curved line is the interpolation threshold. Both thresholds are used to indicate if a variable is predictive of the outcome beyond that of random noise. The variable importance values of the known significant variables are shown to exceed that of the noise and interpolation thresholds.

Fig 5. Comparison of TNBC and simulated data.

(a) An image from the TNBC data and (b) an image from the simulated data. Different colors indicate one of the 16 different cell phenotypes, showing the comparability of the simulations and true data.

Fig 6. No relationship simulation.

Simulation of 16 cell types for 34 patients with meta-variable age. (a) Figure with the variable importance values for all variables. (b) Figure with only the top 25 largest variable importance values. All variables were generated with no-relationship to the outcome and all were determined to have no relation to the outcome beyond noise as the variable importance estimates are below noise and interpolation thresholds.

Fig 7. Relationship simulation.

Simulation of 16 cell types for 34 patients with meta-variable age. (a) Figure with the variable importance values for all variables. (b) Figure with only the top 25 largest variable importance values. Most cell types were generated with no relationship to the outcome. However, age, c1_c2, and c1_c3 were designed to have a relationship with the outcome (which naturally means c2_c2 and c2_c3 would also have relationships to the outcomes). These variables are seen with significantly larger variable importance values than the thresholds and other variable importance values.

Fig 8. Power curves.

Power curves showing the empirical rate, from 100 simulations, that the variable importance for the spatial interaction c1_c2 exceeded the 95% noise threshold, interpolation threshold and both the noise and interpolation thresholds, indicating a significant spatial interaction is detected. The curves indicate the threshold method: above both thresholds (teal), above the curved interpolation threshold (orange), and straight noise threshold (red) (the colours correspond with the noise curves used in the variable importance plots). The x axis gives the standard deviation parameter controlling the distribution of c2 cells around c1 cells. The vertical black dotted line is the base case, when both classes exhibit the same interactions across all cell types, including the c1_c2 interaction. To the right of this line, c2 cells are less densely clustered around c1 cells, and to the left of the line there is increased clustering around c1 cells. The light horizontal, dotted gray line indicates the desired mis-classification rate when no signal is present (i.e. 0.05). (a) Spatial data with 4 cell types is used to create the curves. (b) Spatial data with 16 cell types is used to create the curves. Both images show the method is effective at correctly detecting when the important interaction does and does not differ between the patient outcomes. This is seen as all lines quickly climb to 1 (perfect detection of a signal) as the standard deviation parameter moves further from the no effect case (vertical line). The size and power is similar between the simulations despite the large increase in total interactions considered.

Fig 9. TNBC variable importance.

Variable importance plot and random forest model summary for predicting “compartmentalized” versus “mixed” tumor types with the TNBC data. (a) Figure with the variable importance values for all variables. (b) Figure with only the top 25 largest variable importance values. The OOB far exceeds those of naïve models, and many of the spatial interactions between tumor cells and immune cell populations exhibited significant variable importance values, suggesting important interactions in the data (such as Tumor_Tumor).

Fig 10. Example TNBC K functions.

The K functions from the different outcomes are compared in these two plots. In both plots, the x-axis indicates the radial distance, r, in micrometers and the y-axis is the value of the K function. The lightly colored lines are the K functions for each patient, while the bold lines indicates the average (point-wise mean). In the figures, red indicates the mixed tumors while blue indicates the compartmentalized tumors. The black dashed line indicates the curve of a totally spatially random process for reference. (a) Plots the K functions for the Tumor_Tumor interaction, which was found to have significant differences in the outcomes. (b) Plots the K functions for the CD4T_Endothelial interaction, which was found have no significant differences between the outcomes. In (a), as expected, the compartmentalized group has relatively larger K functions–indicating increased clustering–and the functions are well grouped together. Conversely, (b) shows no clear differences between the K functions of the two groups and K functions are generally surrounded by K functions from patients of an assortment of the groups. That is, K function patterns vary widely even within the same outcome groups.

Fig 11. Lung cancer variable importances.

Variable importance plot and random forest model summary for predicting LUAD versus LUSC tumor types. (a) Figure with the variable importance values for all variables. (b) Figure with only the top 25 largest variable importance values. The OOB is similar to a naïve model, and none of the measured variable importance value were statistically significant, indicating no significant variable interactions or meta-variables.