Sampling bias corrections for accurate neural measures of redundant, unique, and synergistic information

Abstract

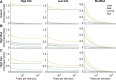
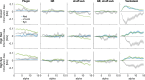
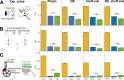
Shannon Information theory has long been a tool of choice to measure empirically how populations of neurons in the brain encode information about cognitive variables. Recently, Partial Information Decomposition (PID) has emerged as principled way to break down this information into components identifying not only the unique information carried by each neuron, but also whether relationships between neurons generate synergistic or redundant information. While it has been long recognized that Shannon information measures on neural activity suffer from a (mostly upward) limited sampling estimation bias, this issue has largely been ignored in the burgeoning field of PID analysis of neural activity. We used simulations to investigate the limited sampling bias of PID computed from discrete probabilities (suited to describe neural spiking activity). We found that PID suffers from a large bias that is uneven across components, with synergy by far the most biased. Using approximate analytical expansions, we found that the bias of synergy increases quadratically with the number of discrete responses of each neuron, whereas the bias of unique and redundant information increase only linearly or sub-linearly. Based on the understanding of the PID bias properties, we developed simple yet effective procedures that correct for the bias effectively, and that improve greatly the PID estimation with respect to current state-of-the-art procedures. We apply these PID bias correction procedures to datasets of 53117 pairs neurons in auditory cortex, posterior parietal cortex and hippocampus of mice performing cognitive tasks, deriving precise estimates and bounds of how synergy and redundancy vary across these brain regions.

Figure 1:

Joint information and PID quantities as a function of the number of simulated trials used to compute them. Top, central and bottom rows plot the simulated scenarios with no interaction, high redundancy and high synergy, respectively (see SM Section SM1.5). Left, center and right columns represent simulations with higher information ($\alpha =10$), lower information $(\alpha =7)$ and with shuffled low-information data. “Syn”: synergy. “Red”: redundancy. “U1+U2”: sum of the two unique information of each neuron. Here we used the plugin method without bias corrections. We used $R=4$ discretization bins for each neuron (Table S1). Each panel plots mean ± 2 SEM over $n=96$ simulations.

Figure 2:

Performance of bias corrections with 4 discretization bins for each neuron. Joint information and PID quantities as a function of the number of simulated trials used to compute them. Top, central and bottom rows plot the simulated scenario with no interaction, high redundancy and high synergy, respectively (see SM Section SM1.5). Left to right columns report results of the QE, shuffle-subtraction, QE with shuffle-subtraction, and Venkatesh procedures, respectively. In each panel we plot the mean ± 2 SEM over $n=96$ simulations.

Figure 3:

Performance of bias corrections using $N_s=64$ trials per stimulus with 4 discretization bins for each neuron. In each panel we plot (rather than the information component value itself) the information component bias (computed as the information component estimated with the considered number of simulated trials minus the asymptotic information component estimated using the largest available number of simulated trials, that is 2048 trials per stimulus) as a function of the parameter $\alpha$ increasing single-neuron information in the simulated data. Top, central and bottom rows plot the simulated scenario with no interaction, high redundancy and high synergy, respectively (see SM Section SM1.5). Left to right columns report results with plugin estimators and with the QE, shuffle-subtraction, QE with shuffle-subtraction, and Venkatesh procedures, respectively. In each panel we plot mean ± 2 SEM over $n=96$ simulations.

Figure 4:

PID bias corrections on real neural data. Each panel plots mean ± 2 SEM over all analyzed simultaneously recorded neural pairs ($n=6209,10750,36158$ for auditory cortex (top row), posterior parietal cortex (middle) and hippocampus (bottom) of joint information, synergy and Redundancy. Mean number $N_s$ of available trials per stimulus per dataset was 70, 100, and 72, respectively. Columns from left to right plot: schematic of each task; results with plugin, QE, shuffle-subtraction, QE with shuffle subtraction respectively. Comparisons between synergy and redundancy were performed with a two-tailed paired t-test (***p < 0.001, n.s.:p > 0.05).