This is a preprint.
A mathematical model for ketosis-prone diabetes suggests the existence of multiple pancreatic β-cell inactivation mechanisms
- PMID: 38895272
- PMCID: PMC11185683
- DOI: 10.1101/2024.06.04.597343
A mathematical model for ketosis-prone diabetes suggests the existence of multiple pancreatic β-cell inactivation mechanisms
Update in
-
A mathematical model for ketosis-prone diabetes suggests the existence of multiple pancreatic β-cell inactivation mechanisms.Elife. 2025 Jul 15;13:RP100193. doi: 10.7554/eLife.100193. Elife. 2025. PMID: 40662943 Free PMC article.
Abstract
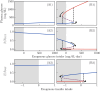
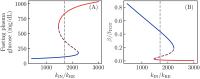
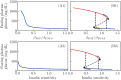
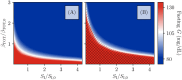
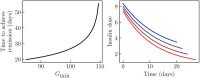
Ketosis-prone diabetes mellitus (KPD) is a subtype of type 2 diabetes, which presents much like type 1 diabetes, with dramatic hyperglycemia and ketoacidosis. Although KPD patients are initially insulin-dependent, after a few months of insulin treatment, roughly 70% undergo near-normoglycemia remission and can maintain blood glucose without insulin, as in early type 2 diabetes or prediabetes. Here, we propose that these phenomena can be explained by the existence of a fast, reversible glucotoxicity process, which may exist in all people but be more pronounced in those susceptible to KPD. We develop a simple mathematical model of the pathogenesis of KPD, which incorporates this assumption, and show that it reproduces the phenomenology of KPD, including variations in the ability for patients to achieve and sustain remission. These results suggest that a variation of our model may be able to quantitatively describe variations in the course of remission among individuals with KPD.
Figures
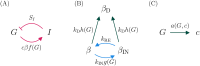

Similar articles
-
A mathematical model for ketosis-prone diabetes suggests the existence of multiple pancreatic β-cell inactivation mechanisms.Elife. 2025 Jul 15;13:RP100193. doi: 10.7554/eLife.100193. Elife. 2025. PMID: 40662943 Free PMC article.
-
Prescription of Controlled Substances: Benefits and Risks.2025 Jul 6. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2025 Jul 6. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 30726003 Free Books & Documents.
-
The Black Book of Psychotropic Dosing and Monitoring.Psychopharmacol Bull. 2024 Jul 8;54(3):8-59. Psychopharmacol Bull. 2024. PMID: 38993656 Free PMC article. Review.
-
Sexual Harassment and Prevention Training.2024 Mar 29. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. 2024 Mar 29. In: StatPearls [Internet]. Treasure Island (FL): StatPearls Publishing; 2025 Jan–. PMID: 36508513 Free Books & Documents.
-
Type 1 Diabetes: A Guide to Autoimmune Mechanisms for Clinicians.Diabetes Obes Metab. 2025 Aug;27 Suppl 6(Suppl 6):40-56. doi: 10.1111/dom.16460. Epub 2025 May 15. Diabetes Obes Metab. 2025. PMID: 40375390 Free PMC article. Review.
References
-
- Ader M, Stefanovski D, Kim SP, Richey JM, Ionut V, Catalano KJ, Hucking K, Ellmerer M, Citters GV, Hsu IR, Chiu JD, Woolcott OO, Harrison LN, Zheng D, Lottati M, Kolka CM, Mooradian V, Dittmann J, Yae S, Liu H, et al. Hepatic insulin clearance is the primary determinant of insulin sensitivity in the normal dog. Obesity. 2014; 22(5):1238–1245. doi: 10.1002/oby.20625. - DOI - PMC - PubMed
-
- Alon U. An Introduction to Systems Biology, Design Principles of Biological Circuits. Chapman & Hall/CRC; 2019. doi: 10.1201/9781420011432. - DOI
-
- CDC. Centers for Disease Control and Prevention. National Diabetes Statistics Report, 2020. Atlanta, GA; 2020.
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
