Evolutionary rescue in resistance to pesticides

Abstract

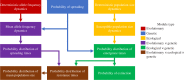
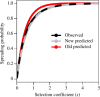
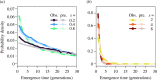
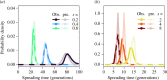
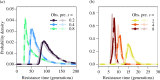
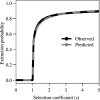
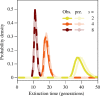
Evolutionary rescue occurs when the genetic evolution of adaptation saves a population from decline or extinction after environmental change. The evolution of resistance to pesticides is a special scenario of abrupt environmental change, where rescue occurs under (very) strong selection for one or a few de novo resistance mutations of large effect. Here, a population genetic model of evolutionary rescue with density-dependent population change is developed, with a focus on deriving results that are important to resistance management. Massive stochastic simulations are used to generate observations, which are accurately predicted using analytical approximations. Key results include the probability density function for the time to resistance and the probability of population extinction. The distribution of resistance times shows a lag period, a narrow peak and a long tail. Surprisingly, the mean time to resistance can increase with the strength of selection because, if a mutation does not occur early on, then its emergence is delayed by the pesticide reducing the population size. The probability of population extinction shows a sharp transition, in that when extinction is possible, it is also highly likely. Consequently, population suppression and (local) eradication can be theoretically achievable goals, as novel strategies to delay resistance evolution.

Keywords: eco-evolutionary dynamics; evolutionary rescue; pesticide resistance; population ecology; population genetics; resistance management.

Figure 1.

Overview of the modules of the continuous-time framework that is used to generate predictions of the key dynamics, distributions and statistics from discrete-time simulations. Colours show how results are derived by integrating approximations from different module types.

Figure 2.

Comparison across selection coefficients of the observed probability of spread in discrete-time simulations (black) and the predicted probability of spread (red) as approximated by the classic expression $1-e^{-2s}$ and as rederived here (grey) in equation (2.5).

Figure 3.

Comparison of the observed probability density function for emergence times in discrete-time simulations (bold colours) and the predicted probability density function for emergence times (faded colours) as approximated in equation (2.21) for (a) lower and (b) higher selection coefficients.

Figure 4.

Comparison of the observed probability density function for spreading times in discrete-time simulations (bold colours) and the predicted probability density function for spreading times (faded colours) as approximated in equation (2.25) for (a) lower and (b) higher selection coefficients.

Figure 5.

Comparison of the observed probability density function for resistance times in discrete-time simulations (bold colours) and the predicted probability density function for resistance times (faded colours) as approximated by the convolution of the predicted probability density functions for emergence and spreading times for (a) lower and (b) higher selection coefficients.

Figure 6.

Comparison across selection coefficients of the observed probability of extinction in discrete-time simulations (black) and the predicted probability of extinction (grey) as approximated by $1-\sum T_{E,t}$ .

Figure 7.

Comparison of the observed probability density function for extinction times in discrete-time simulations (bold colours) and the predicted probability density function for extinction times (faded colours) as approximated in equation (2.26) for higher selection coefficients where extinction is possible.