Network Derivation of Liquid Junction Potentials in Single-Membrane System
- PMID: 38921507
- PMCID: PMC11205610
- DOI: 10.3390/membranes14060140
Network Derivation of Liquid Junction Potentials in Single-Membrane System
Abstract
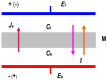
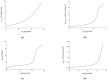
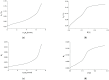
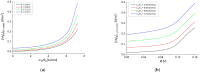
Peusner's network thermodynamics (PNT) is one of the more important formalisms of nonequilibrium thermodynamics used to describe membrane transport and the conversion of the internal energy of the system into energy dissipated in the environment and free energy used for the work involved in the transport of solution components in membrane processes. A procedure of transformation the Kedem-Katchalsky (K-K) equations for the transport of binary electrolytic solutions through a membrane to the Kedem-Katchalsky-Peusner (K-K-P) equations based on the PNT formalism for liquid junction potentials was developed. The subject of the study was a membrane used for hemodialysis (Ultra Flo 145 Dialyser) and aqueous NaCl solutions. The research method was the L version of the K-K-P formalism for binary electrolyte solutions. The Peusner coefficients obtained from the transformations of the K-K formalism coefficients for the transport of electrolyte solutions through the artificial polymer membrane were used to calculate the coupling coefficients of the membrane processes and to calculate the dissipative energy flux. In addition, the dissipative energy flux, as a function of thermodynamic forces, made it possible to investigate the energy conversion of transport processes in the membrane system.
Keywords: Kedem–Katchalsky–Peusner equations; Peusner transport coefficients; S entropy; internal energy conversion; membrane transport; polymeric membrane.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures

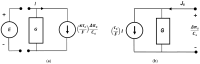





References
-
- Baker R. Membrane Technology and Application. John Wiley & Sons; New York, NY, USA: 2012.
LinkOut - more resources
Full Text Sources

