Influence of Time-Lag Effects between Winter-Wheat Canopy Temperature and Atmospheric Temperature on the Accuracy of CWSI Inversion of Photosynthetic Parameters
- PMID: 38931132
- PMCID: PMC11207421
- DOI: 10.3390/plants13121702
Influence of Time-Lag Effects between Winter-Wheat Canopy Temperature and Atmospheric Temperature on the Accuracy of CWSI Inversion of Photosynthetic Parameters
Abstract
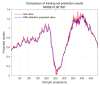
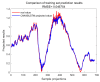
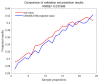
When calculating the CWSI, previous researchers usually used canopy temperature and atmospheric temperature at the same time. However, it takes some time for the canopy temperature (Tc) to respond to atmospheric temperature (Ta), suggesting the time-lag effects between Ta and Tc. In order to investigate time-lag effects between Ta and Tc on the accuracy of the CWSI inversion of photosynthetic parameters in winter wheat, we conducted an experiment. In this study, four moisture treatments were set up: T1 (95% of field water holding capacity), T2 (80% of field water holding capacity), T3 (65% of field water holding capacity), and T4 (50% of field water holding capacity). We quantified the time-lag parameter in winter wheat using time-lag peak-seeking, time-lag cross-correlation, time-lag mutual information, and gray time-lag correlation analysis. Based on the time-lag parameter, we modified the CWSI theoretical and empirical models and assessed the impact of time-lag effects on the accuracy of the CWSI inversion of photosynthesis parameters. Finally, we applied several machine learning algorithms to predict the daily variation in the CWSI after time-lag correction. The results show that: (1) The time-lag parameter calculated using time-lag peak-seeking, time-lag cross-correlation, time-lag mutual information, and gray time-lag correlation analysis are 44-70, 32-44, 42-58, and 76-97 min, respectively. (2) The CWSI empirical model corrected by the time-lag mutual information method has the highest correlation with photosynthetic parameters. (3) GA-SVM has the highest prediction accuracy for the CWSI empirical model corrected by the time-lag mutual information method. Considering time lag effects between Ta and Tc effectively enhanced the correlation between CWSI and photosynthetic parameters, which can provide theoretical support for thermal infrared remote sensing to diagnose crop water stress conditions.
Keywords: CWSI; photosynthetic rate; stomatal conductance; time-lag effects; transpiration rate; winter wheat.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures

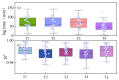
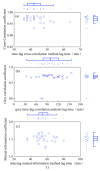













Similar articles
-
Monitoring soil moisture in winter wheat with crop water stress index based on canopy-air temperature time lag effect.Int J Biometeorol. 2024 Apr;68(4):647-659. doi: 10.1007/s00484-023-02612-2. Epub 2024 Jan 3. Int J Biometeorol. 2024. PMID: 38172400
-
Water Deficit Diagnosis of Winter Wheat Based on Thermal Infrared Imaging.Plants (Basel). 2024 Jan 25;13(3):361. doi: 10.3390/plants13030361. Plants (Basel). 2024. PMID: 38337894 Free PMC article.
-
Evaluation of crop water stress index of wheat by using machine learning models.Environ Monit Assess. 2024 Sep 23;196(10):970. doi: 10.1007/s10661-024-13113-z. Environ Monit Assess. 2024. PMID: 39312101
-
Combining thermal imaging and soil water content sensors to assess tree water status in pear trees.Front Plant Sci. 2023 Jun 6;14:1197437. doi: 10.3389/fpls.2023.1197437. eCollection 2023. Front Plant Sci. 2023. PMID: 37346137 Free PMC article.
-
Estimating evapotranspiration and drought stress with ground-based thermal remote sensing in agriculture: a review.J Exp Bot. 2012 Aug;63(13):4671-712. doi: 10.1093/jxb/ers165. J Exp Bot. 2012. PMID: 22922637 Review.
Cited by
-
Introduction to the Special Issue of Plants on "The Application of Spectral Techniques in Agriculture and Forestry".Plants (Basel). 2024 Sep 20;13(18):2632. doi: 10.3390/plants13182632. Plants (Basel). 2024. PMID: 39339603 Free PMC article.
References
-
- Kifle M., Gebretsadikan T.G. Yield and water use efficiency of furrow irrigated potato under regulated deficit irrigation, Atsibi-Wemberta, North Ethiopia. Agric. Water Manag. 2016;170:133–139. doi: 10.1016/j.agwat.2016.01.003. - DOI
-
- Liu E.K., Mei X.R., Yan C.R., Gong D.Z., Zhang Y.Q. Effects of water stress on photosynthetic characteristics, dry matter translocation and WUE in two winter wheat genotypes. Agric. Water Manag. 2016;167:75–85. doi: 10.1016/j.agwat.2015.12.026. - DOI
-
- Saini S., Raj K., Saini A.K., Kumar R., Saini A., Khan A., Kumar P., Devi G., Bhambhu M.K., McKenzie C.L., et al. Unravelling the synergistic interaction of Thrips tabaci and newly recorded, Thrips parvispinus with Alternaria porri (Ellis.) Cif., inciting onion purple blotch. Front. Microbiol. 2024;15:1321921. doi: 10.3389/fmicb.2024.1321921. - DOI - PMC - PubMed
-
- Carrasco-Benavides M., Espinoza-Meza S., Umemura K., Ortega-Farías S., Baffico-Hernández A., Neira-Román J., Ávila-Sánchez C., Fuentes S. Evaluation of thermal-based physiological indicators for determining water-stress thresholds in drip-irrigated ‘Regina’ cherry trees. Irrig. Sci. 2024;42:445–459. doi: 10.1007/s00271-024-00916-8. - DOI
LinkOut - more resources
Full Text Sources

