Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jul 16;51(9):1772-1791.
doi: 10.1080/02664763.2023.2235093. eCollection 2024.

A hierarchical Bayesian analysis for bivariate Weibull distribution under left-censoring scheme

Danielle Peralta  1 , Ricardo Puziol de Oliveira  2 , Jorge Alberto Achcar  1
Affiliations

A hierarchical Bayesian analysis for bivariate Weibull distribution under left-censoring scheme

Danielle Peralta et al. J Appl Stat. .

Abstract

This paper presents a novel approach for analyzing bivariate positive data, taking into account a covariate vector and left-censored observations, by introducing a hierarchical Bayesian analysis. The proposed method assumes marginal Weibull distributions and employs either a usual Weibull likelihood or Weibull-Tobit likelihood approaches. A latent variable or frailty is included in the model to capture the possible correlation between the bivariate responses for the same sampling unit. The posterior summaries of interest are obtained through Markov Chain Monte Carlo methods. To demonstrate the effectiveness of the proposed methodology, we apply it to a bivariate data set from stellar astronomy that includes left-censored observations and covariates. Our results indicate that the new bivariate model approach, which incorporates the latent factor to capture the potential dependence between the two responses of interest, produces accurate inference results. We also compare the two models using the different likelihood approaches (Weibull or Weibull-Tobit likelihoods) in the application. Overall, our findings suggest that the proposed hierarchical Bayesian analysis is a promising approach for analyzing bivariate positive data with left-censored observations and covariate information.

Keywords: Bayesian analysis; Tobit model; Weibull distribution; left-censored data; stellar data.

PubMed Disclaimer

Conflict of interest statement

No potential conflict of interest was reported by the author(s).

Figures

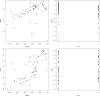
Figure 1.
Figure 1.
Scatterplots of log(Be) (upper panels) and log(Li) (lower panels) versus Type and log( Teff).
Figure 2.
Figure 2.
Half-normal plot for residuals of the fitted proposed Weibull regression model for the responses Be (left panel) and Li (right panel).
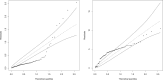
Figure 3.
Figure 3.
Half-normal plot for residuals of the fitted proposed Weibull–Tobit regression model for the responses Be (left panel) and Li (right panel).
See this image and copyright information in PMC

References

    1. Aalen O., Borgan O., and Gjessing H., Survival and Event History Analysis: a Process Point of View, Springer Science & Business Media, 2008.
    1. Achcar J.A., Coelho-Barros E.A., and Mazucheli J., Cure fraction models using mixture and non-mixture models, Tatra Mt. Math. Publ. 51 (2012), pp. 1–9.
    1. Aitkin M., Posterior Bayes factors, J. R. Stat. Soc. B Methodol. 53 (1991), pp. 111–128.
    1. Almetwally E.M., Muhammed H.Z., and El-Sherpieny E.S.A., Bivariate Weibull distribution: properties and different methods of estimation, Ann. Data Sci. 7 (2020), pp. 163–193.
    1. Arnold B.C. and Strauss D., Bivariate distributions with exponential conditionals, J. Am. Stat. Assoc. 83 (1988), pp. 522–527.

LinkOut - more resources