Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Jul 12;51(9):1642-1663.
doi: 10.1080/02664763.2023.2230533. eCollection 2024.

The generalized odd log-logistic-G regression with interval-censored survival data

Valdemiro P Vigas  1 , Edwin M M Ortega  2 , Adriano K Suzuki  3 , Gauss M Cordeiro  4 , Paulo C Dos Santos Junior  5
Affiliations

The generalized odd log-logistic-G regression with interval-censored survival data

Valdemiro P Vigas et al. J Appl Stat. .

Abstract

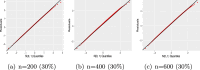
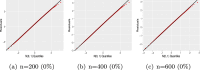
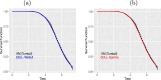
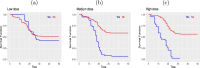
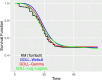
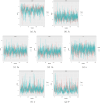
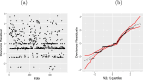
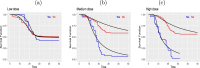
The article proposes a new regression based on the generalized odd log-logistic family for interval-censored data. The survival times are not observed for this type of data, and the event of interest occurs at some random interval. This family can be used in interval modeling since it generalizes some popular lifetime distributions in addition to its ability to present various forms of the risk function. The estimation of the parameters is addressed by the classical and Bayesian methods. We examine the behavior of the estimates for some sample sizes and censorship percentages. Selection criteria, likelihood ratio tests, residual analysis, and graphical techniques assess the goodness of fit of the fitted models. The usefulness of the proposed models is red shown by means of two real data sets.

Keywords: 62N01; Bayesian inference; generalized odd log-logistic family; interval-censored data; regression model; residual analysis.

PubMed Disclaimer

Conflict of interest statement

No potential conflict of interest was reported by the author(s).

Figures

Figure 1.
Figure 1.
Plots of the hrf for the GOLL-W model.
Figure 2.
Figure 2.
QQ-plots for the deviance residuals in the GOLL-LL regression with 30% censoring percentages.
Figure 3.
Figure 3.
QQ-plots for the deviance residuals in the GOLL-LL regression with 0% censoring percentages.
Figure 4.
Figure 4.
Estimated survival functions for the fitted model and the empirical survival function. (a) GOLL-W distribution and (b) GOLL-Ga distribution.
Figure 5.
Figure 5.
Estimated survival curves by Turnbull's method for the covariates: (a) low dose, (b) medium dose and (c) high dose.
Figure 6.
Figure 6.
Estimated survival functions for the fitted GOLL-W, GOLL-Ga and GOLL-LL distributions and the empirical survival function.
Figure 7.
Figure 7.
Traceplots for the parameters of the regression M2. (a) β0, (b) β1, (c) β2; (a) β3, (b) a, (c) α, (d) θ.
Figure 8.
Figure 8.
Residual plots for the regression M2. (a) Deviance residuals and (b) Normal probability plot for the deviance residuals with envelope.
Figure 9.
Figure 9.
Estimated survival functions and the empirical survival curve for the covariates: (a) low dose, (b) medium dose and (c) high dose.
See this image and copyright information in PMC

References

    1. Alizadeh M., Korkmaz M.Ç., Almamy J.A., and Ahmed A.A.E., Another odd log-logistic logarithmic class of continuous distributions, Istatistikçiler Dergisi: Istatistik & Aktuerya 11 (2018), pp. 55–72.
    1. Atkinson A.C., Two graphical displays for outlying and influential observations in regression, Biometrika 68 (1981), pp. 13–20.
    1. Basak P., Linero A.R., Sinha D., and Lipsitz S., Semiparametric analysis of clustered interval-censored survival data using soft Bayesian additive regression trees (sbart), Biometrics 78 (2021), pp. 1–14. - PubMed
    1. Betensky R.A. and Finkelstein D.M., Testing for dependence between failure time and visit compliance with interval-censored data, Biometrics 58 (2002), pp. 58–63. - PubMed
    1. Bogaerts K. and Lesaffre E., Estimating local and global measures of association for bivariate interval censored data with a smooth estimate of the density, Stat. Med. 27 (2008), pp. 5941–5955. - PubMed

LinkOut - more resources