Global dynamics and computational modeling for analyzing and controlling Hepatitis B: A novel epidemic approach

Abstract

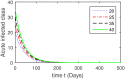
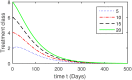
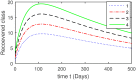
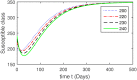
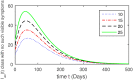
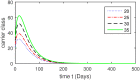
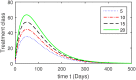
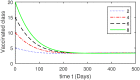
Hepatitis B virus (HBV) infection is a global public health issue. We offer a comprehensive analysis of the dynamics of HBV, which can be successfully controlled with vaccine and treatment. Hepatitis B virus (HBV) causes a significantly more severe and protracted disease compared to hepatitis A. While it initially presents as an acute disease, in approximately 5 to 10% of cases, it can develop into a chronic disease that causes permanent damage to the liver. The hepatitis B virus can remain active outside the body for at least seven days. If the virus penetrates an individual's body without immunization, it may still result in infection. Upon exposure to HBV, the symptoms often last for a duration ranging from 10 days to 6 months. In this study, we developed a new model for Hepatitis B Virus (HBV) that includes asymptomatic carriers, vaccination, and treatment classes to gain a comprehensive knowledge of HBV dynamics. The basic reproduction number [Formula: see text] is calculated to identify future recurrence. The local and global stabilities of the proposed model are evaluated for values of [Formula: see text] that are both below and above 1. The Lyapunov function is employed to ensure the global stability of the HBV model. Further, the existence and uniqueness of the proposed model are demonstrated. To look at the solution of the proposed model graphically, we used a useful numerical strategy, such as the non-standard finite difference method, to obtain more thorough numerical findings for the parameters that have a significant impact on disease elimination. In addition, the study of treatment class in the population, we may assess the effectiveness of alternative medicines to treat infected populations can be determined. Numerical simulations and graphical representations are employed to illustrate the implications of our theoretical conclusions.

Fig 1. Flowchart illustrating the transmission model of Hepatitis B Virus (HBV).

Fig 2. Graphical presentation of S class using different values of the parameters.

Fig 3. Graphical presentation of L class using different values of the parameters.

Fig 4. Graphical presentation of I_a class using different values of the parameters.

Fig 5. Graphical presentation of I_ac using different values of the parameters.

Fig 6. Graphical presentation of I_a using different values of the parameters.

Fig 7. Graphical presentation of T using different values of the parameters.

Fig 8. Graphical presentation of V using different values of the parameters.

Fig 9. Graphical presentation of R using different values of the parameter.

Fig 10. Susceptible class using the numerical scheme when β = 0.0009.

Fig 11. Graphical presentation of latently infected class using the numerical scheme when ∏ = 5.5 and β = 0.0009.

Fig 12. Graphical presentation of acute infected class using the numerical scheme when ∏ = 5.5 and β = 0.0009.

Fig 13. Graphical presentation of asymptotically infected class with no visible symptoms using the numerical scheme when ∏ = 5.5 and β = 0.0009.

Fig 14. Graphical presentation of carrier-class using the numerical scheme when ∏ = 5.5 and β = 0.0009.

Fig 15. Graphical presentation of treatment class using the numerical scheme when ∏ = 5.5 and β = 0.0009.

Fig 16. Graphical presentation of vaccinated class using the numerical scheme when ∏ = 5.5 and β = 0.0009.

Fig 17. Graphical presentation of recovered class using the numerical scheme when ∏ = 5.5 and β = 0.0009.