Application of physics encoded neural networks to improve predictability of properties of complex multi-scale systems

Abstract

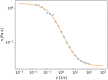
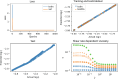
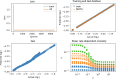
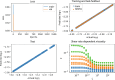
Predicting physical properties of complex multi-scale systems is a common challenge and demands analysis of various temporal and spatial scales. However, physics alone is often not sufficient due to lack of knowledge on certain details of the system. With sufficient data, however, machine learning techniques may aid. If data are yet relatively cumbersome to obtain, hybrid methods may come to the rescue. We focus in this report on using various types of neural networks (NN) including NN's into which physics information is encoded (PeNN's) and also studied effects of NN's hyperparameters. We apply the networks to predict the viscosity of an emulsion as a function of shear rate. We show that using various network performance metrics as the mean squared error and the coefficient of determination ( $R^2$ ) that the PeNN's always perform better than the NN's, as also confirmed by a Friedman test with a p-value smaller than 0.0002. The PeNN's capture extrapolation and interpolation very well, contrary to the NN's. In addition, we have found that the NN's hyperparameters including network complexity and optimization methods do not have any effect on the above conclusions. We suggest that encoding NN's with any disciplinary system based information yields promise to better predict properties of complex systems than NN's alone, which will be in particular advantageous for small numbers of data. Such encoding would also be scalable, allowing different properties to be combined, without repetitive training of the NN's.

Keywords: Complex systems; Machine learning; Multi-scale modeling; Neural networks; Physics encoded neural networks.

Figure 1

Example of a flow curve of an oil-in-water emulsion and Quemada-model-fit.

Figure 2

Schematic architecture of the NN (left, middle) and PeNN (right) configuration.

Figure 3

Schematic architecture of the NN (left, middle) and PeNN (right) configuration.

Figure 4

Results of the NN 2-128-32-8-1 neural network (see Fig. 3). This NN was trained and tested using a data set generated from $n=3$ different ${\varphi }_p$ and for each ${\varphi }_p$ $N=300$ different $\dot{\gamma }$. Top-left: loss as a function of number of epochs; Top-right: predicted versus actual values of the training (blue) and test-holdout (orange) set; Bottom-left: predicted versus ground truth of the test set containing unseen ${\varphi }_p$; Bottom-right: examples of ground truth (actual) shear rate dependent viscosity ($\circ$ (seen ${\varphi }_p$) and $\square$ (unseen ${\varphi }_p$)) and predicted shear rate dependent viscosity ($\bullet$). The colors indicate different ${\varphi }_p$.

Figure 5

Results of the PeNN 2-1-1-1 [physical-encoded neural network (see Fig. 3). This NN was trained and tested using a data set generated from $n=3$ different ${\varphi }_p$ and for each ${\varphi }_p$ $N=300$ different $\dot{\gamma }$. Top-left: loss as a function of number of epochs; Top-right predicted versus actual values of the training (blue) and test-holdout (orange) set; Bottom-left: predicted versus actual values of the test set containing unseen ${\varphi }_p$; Bottom-right: examples of actual shear rate dependent viscosity ($\circ$ (seen ${\varphi }_p$) and $\square$ (unseen ${\varphi }_p$)) and predicted shear rate dependent viscosity ($\bullet$). The colors indicate different ${\varphi }_p$.

Figure 6

Results of the NN 4-32-8-1 neural network (see Fig. 3). The NN was trained and tested using a data set generated from $n=3$ different ${\varphi }_p$ and for each ${\varphi }_p$ $N=300$ different $\dot{\gamma }$. Top-left: loss as a function of number of epochs; Top-right predicted versus actual values of the training and test-holdout set; Bottom-left: predicted versus actual values of the test set; Bottom-right: examples of actual shear rate dependent viscosity ($\circ$ (seen ${\varphi }_p$) and $\square$ (unseen ${\varphi }_p$)) and predicted shear rate dependent viscosity ($\bullet$). The colors indicate different ${\varphi }_p$.

Figure 7

Results of the PeNN 4-6-2-1-1-1 physical-encoded neural network (see Fig. 3). The PeNN was trained and tested using a data set generated from $n=3$ different ${\varphi }_p$ and for each ${\varphi }_p$ $N=300$ different $\dot{\gamma }$. Top-left: loss as a function of number of epochs; Top-right: predicted versus actual values of the training (orange) and test-holdout (blue) set; Bottom-left: predicted versus actual values of the test set ${\varphi }_p$; Bottom-right: examples of actual ($\circ$) and predicted ($\bullet$) flow curves (colors indicate ${\varphi }_p$.

Figure 8

Mean squared error (mse) of the different NN’s and PeNN between predicted and ground truth values for the test set. The colors correspond to NN 4-32-8-1 (blue), NN 4-128-32-8-1 (orange), and PeNN 4-6-2-1-1-1 (green). The horizontal axis correspond to different data sets generated with $n\in [3,5,7]$ different ${\varphi }_p$’s and for each ${\varphi }_p$, $N\in [20,50,100,300,500]$ different $log\dot{\gamma }$.