Plume-scale confinement on thermal convection

Abstract

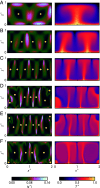
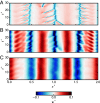
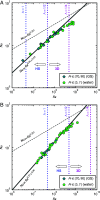
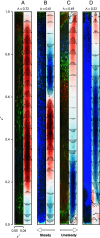
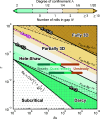
Despite the ubiquity of thermal convection in nature and artificial systems, we still lack a unified formulation that integrates the system's geometry, fluid properties, and thermal forcing to characterize the transition from free to confined convective regimes. The latter is broadly relevant to understanding how convection transports energy and drives mixing across a wide range of environments, such as planetary atmospheres/oceans and hydrothermal flows through fractures, as well as engineering heatsinks and microfluidics for the control of mass and heat fluxes. Performing laboratory experiments in Hele-Shaw geometries, we find multiple transitions that are identified as remarkable shifts in flow structures and heat transport scaling, underpinning previous numerical studies. To unveil the mechanisms of the geometrically controlled transition, we focus on the smallest structure of convection, posing the following question: How free is a thermal plume in a closed system? We address this problem by proposing the degree of confinement [Formula: see text]-the ratio of the thermal plume's thickness in an unbounded domain to the lateral extent of the system-as a universal metric encapsulating all the physical parameters. Here, we characterize four convective regimes different in flow dimensionality and time dependency and demonstrate that the transitions across the regimes are well tied with [Formula: see text]. The introduced metric [Formula: see text] offers a unified characterization of convection in closed systems from the plume's standpoint.

Keywords: heat transport; hydrothermal systems; thermal convection.

Fig. 1.

Instantaneous velocity fields (Left) and mean temperature fields (Right) in the HS cell of $\mathrm{\Gamma }=0.02$ for water, $Pr\in [5,7]$: (A) $Ra=1.7\times {10}^7$ ($\mathrm{\Lambda }=1.35$, two cells), (B) $Ra=2.0\times {10}^7$ ($\mathrm{\Lambda }=1.28$, four cells), (C) $Ra=6.3\times {10}^7$ ($\mathrm{\Lambda }=0.91$, six cells), (D) $Ra=1.7\times {10}^8$ ($\mathrm{\Lambda }=0.68$, unsteady plumes), (E) $Ra=2.9\times {10}^8$ ($\mathrm{\Lambda }=0.58$, unsteady plumes) and (F) $Ra=4.1\times {10}^8$ ($\mathrm{\Lambda }=0.52$, large-scale circulations). Circles are perceptual centers of closed convective cells. See Movies S1–S3 for videos of (D–F).

Fig. 2.

Timeline of $w^{\ast }$ at (A) $z^{\ast }=0.97$, (B) $0.80$, and (C) $0.50$ for $\mathrm{\Lambda }=0.58$ ($\mathrm{\Gamma }=0.02$, $Pr=6.4$, and $Ra=2.9\times {10}^8$). The condition corresponds to Fig. 1E.

Fig. 3.

$\mathit{Nu}$ vs. $\mathit{Ra}$ for (A) $\mathrm{\Gamma }=0.04$ and (B) $\mathrm{\Gamma }=0.02$. Values of $\mathit{Pr}$ are displayed by different markers. The solid line is the best power-law fit for the present data points $Ra\le 1.0\times {10}^8$. The dashed line represents the best fit, $Nu\propto 0.14P{r}^{-0.03}R{a}^{0.297}$ with $Pr=7$, obtained in a large vessel $\mathrm{\Lambda }\ll 1$ (62). The dotted vertical lines are the $\mathit{Ra}$ values corresponding to $\mathrm{\Lambda }=1/4$, $1/2$, and $1$. The datasets are available in SI Appendix, Table 1.

Fig. 4.

Visualization of flow structures in gap-wise vertical cross-sections for $\mathrm{\Gamma }=1/25$ qualitative temperature field visualized using TLC particles (Left) and velocity field measured by particle image velocimetry (Right): (A) $\mathrm{\Lambda }=0.72$ ($Ra=1.78\times {10}^7$ and $Pr=87.9$), (B) $\mathrm{\Lambda }=0.61$ ($Ra=2.39\times {10}^7$ and $Pr=7.0$), (C) $\mathrm{\Lambda }=0.49$ ($Ra=6.54\times {10}^7$ and $Pr=88.4$), and (D) $\mathrm{\Lambda }=0.22$ ($Ra=7.65\times {10}^8$ and $Pr=5.7$). The colormaps in the Right panels represent $w$ scaled by the maximum vertical velocity in each plane.

Fig. 5.

Phase diagram of RBC in a closed system under the geometrically controlled transition. The background color represents the degree of confinement $\mathrm{\Lambda }$ mapped in the $\mathit{Ra}$-$\mathrm{\Gamma }$ domain, and the flow states observed in the experiments are shown by the thick horizontal lines. Here, $\mathrm{\Lambda }$ is computed using $c=0.14$, $\beta =-0.03$, and $\gamma =0.297$ (62). The solid lines highlight $\mathrm{\Lambda }=2$, $1/2$, and $1/20$, corresponding to the regime transitions. The dotted line is the $\mathrm{\Gamma }$-dependent critical Rayleigh number, $R{a}_{\mathrm{c}}\approx {(2\pi )}^4[1+1/(4{\mathrm{\Gamma }}^2)]$ (78), which sets the “subcritical regime” (hatched by dots). The dashed line, ${\mathrm{\Gamma }}_{\mathrm{D}}={(6/5)}^{1/2}R{a}^{-1/4}$, is the empirical Upper limit to recover characteristics of Darcy convection (15) (hatched by crosses), approximately overlaps $\mathrm{\Lambda }=2$. In the “Darcy regime,” $\mathrm{\Lambda }>2$, the heat transport scaling exponent recovers that in Darcy convection, $\gamma \approx 1$ (4, 63). The “Hele-Shaw regime” is identified as $1/2<\mathrm{\Lambda }<2$, where the scaling exponent is $\mathrm{\Gamma }$-dependent and steady Poiseuille-like flows develop. The flow turns to be 3D only at the boundaries when $1/20<\mathrm{\Lambda }<1/2$, establishing the “partially 3D regime.” The system does not exhibit significant differences in flow structures and heat transport scaling from those in unbounded convection in the “fully 3D regime” (hatched by diagonal crosses) when $\mathrm{\Lambda }<1/20$. The empirical border ${\mathrm{\Gamma }}_{3\mathrm{D}}=12.42R{a}^{-0.21}$ (the dashed line) proposed in ref. approximately coincides with $\mathrm{\Lambda }=1/20$. The dashed line for ${\mathrm{\Gamma }}_{\mathrm{opt}}=29.37R{a}^{-0.31}$ denotes the empirical fitting for the optimal heat transport where the $\mathit{Nu}$ is maximized for a given $\mathit{Ra}$ (14, 47), coinciding with $\mathrm{\Lambda }=1/6$.