Terahertz magnetic response of plasmonic metasurface resonators: origin and orientation dependence

Abstract

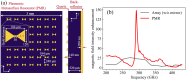
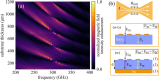
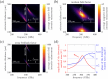
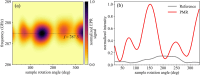
The increasing miniaturization of everyday devices necessitates advancements in surface-sensitive techniques to access phenomena more effectively. Magnetic resonance methods, such as nuclear or electron paramagnetic resonance, play a crucial role due to their unique analytical capabilities. Recently, the development of a novel plasmonic metasurface resonator aimed at boosting the THz electron magnetic response in 2D materials resulted in a significant magnetic field enhancement, confirmed by both numerical simulations and experimental data. Yet, the mechanisms driving this resonance were not explored in detail. In this study, we elucidate these mechanisms using two semi-analytical models: one addressing the resonant behaviour and the other examining the orientation-dependent response, considering the anisotropy of the antennas and experimental framework. Our findings contribute to advancing magnetic spectroscopic techniques, broadening their applicability to 2D systems.

Keywords: Cavity-enhanced; Electron paramagnetic resonance; Fabry-Pérot; Magnetic metasurface; Terahertz.

Figure 1

(a) Design parameters of the PMR. (b) Resonance intensity of the in-plane magnetic field intensity enhancement of the PMR (array and back-reflector) and array without back-reflector obtained by numerical simulations. The near-field intensities were determined 10 nm above the antennas top plane and rescaled by the source intensity to obtain the field enhancement. More details in reference.

Figure 2

(a) Map of normalized in-plane magnetic field intensity enhancement of the PMR simulated as a function of frequency and substrate thickness. The simulation was performed with CST Microwave Studio using the parameters in Fig. 1a. (b) Scheme and parameters used in the semi-analytical model (see text).

Figure 3

(a) Map of the average magnetic field intensity enhancement as a function of frequency and substrate thickness calculated by our semi-analytical model, which reproduces the dispersion branches observed in Fig. 2. (b) Map of the average magnetic field intensity enhancement based solely on the incident field factor incorporating only the effect of the quartz/gold interface on the illuminating wave. (c) Map of the average magnetic field intensity enhancement utilizing only the array feedback factor (i.e., $E_{\text{re}}^{(w)}\left(\omega \right)$), which captures the interaction of the array with itself. The intersection of the white dotted lines in all the maps marks the gap in the dispersion branch due to the complete destructive interference between the forward propagating incident wave and its back-reflected counterpart. (d) Amplitude and phase of the wave emitted into the quartz substrate by the antenna array as a function of frequency obtained by FDTD simulations.

Figure 4

(a) Experimental map of the magnetic resonance of TEMPOL radical, centred at the resonant frequency of the PMR (287.5 GHz, see text), as a function of the frequency and of the angle between the PMR and the incident electric field vector, measured in a constant magnetic field of 10.22 T and a temperature of 10 K. (b) Angular profile taken at the frequency of 287.5 GHz for the sample deposited on the PMR (red) and on a bare quartz substrate (grey, reference).

Figure 5

(a) Schematics of the simplified optical path considered in our theoretical model. After passing the first polarizer, radiation interacts with the sample and is reflected from the PMR. Before it reaches the detector, it once again passes through the magnetic layer and is filtered by the second polarizer. Sample, PMR and mirror are separated for clarity. (b) Intensity map of the EPR signal as a function of the frequency and the angle formed by the long axis of the diabolo antennas and the plane of polarization of the illuminating wave. The map was calculated using our theoretical model, with input parameters based on simulations of a PMR exhibiting optimal performance. The angular profile at the bottom corresponds to a cut along the white dotted line in the intensity map and is shown together with the experiment for comparison. The pictograms show the mutual orientation of the diabolo antenna and the incident electric field vector for several significant values of the angle $\theta$. (c) Same as in (b), except the phase shift ${\varphi }_{\text{bg}}-{\varphi }_{\text{array}}$ between the field amplitudes $r_{\text{bg}}$ and $r_{\text{array}}$ was artificially set to 3$\pi /4$. Apparently, the departure from the ideal resonance of the PMR can lift the conditions that prevented Faraday effect from manifesting and break the original four-fold symmetry of the angular profile.