Necking of thin-walled cylinders via bifurcation of incompressible nonlinear elastic solids

Abstract

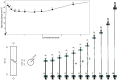
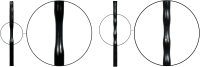
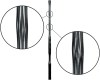
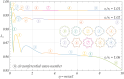
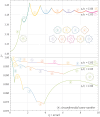
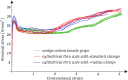
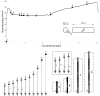
Necking localization under quasi-static uniaxial tension is experimentally observed in ductile thin-walled cylindrical tubes, made of soft polypropylene. Necking nucleates at multiple locations along the tube and spreads throughout, involving the occurrence of higher-order modes, evidencing trefoil and fourth-foiled (but rarely even fifth-foiled) shaped cross-sections. No evidence of such a complicated necking occurrence and growth was found in other ductile materials for thin-walled cylinders under quasi-static loading. With the aim of modelling this phenomenon, as well as all other possible bifurcations, a two-dimensional formulation is introduced, in which only the mean surface of the tube is considered, paralleling the celebrated Flügge 's treatment of axially-compressed cylindrical shells. This treatment is extended to include tension and a broad class of nonlinear-hyperelastic constitutive law for the material, which is also assumed to be incompressible. The theoretical framework leads to a number of new results, not only for tensile axial force (where necking is modelled and, as a particular case, the classic Considère formula is shown to represent the limit of very thin tubes), but also for compressive force, providing closed-form formulae for wrinkling (showing that a direct application of the Flügge equation can be incorrect) and for Euler buckling. It is shown that the J₂-deformation theory of plasticity (the simplest constitutive assumption to mimic through nonlinear elasticity the plastic branch of a material) captures multiple necking and occurrence of higher-order modes, so that experiments are explained. The presented results are important for several applications, ranging from aerospace and automotive engineering to the vascular mechanobiology, where a thin-walled tube (for instance an artery, or a catheter, or a stent) may become unstable not only in compression, but also in tension.

Fig. 1. Nominal stress vs. conventional strain obtained from a tensile test on a polypropylene (PP) thin-walled tube (6.5 mm initial diameter, 0.18 mm thickness, 205 mm length). During the test, the sample was brought up to a conventional strain of 4.5 at which the test was terminated before failure. The final thickness of the tube wall was 0.06 mm. Initiation and progression of necking is documented in Fig. 2.

Fig. 2. Nucleation and development of multiple necks in polypropylene (PP) thin-walled tubes pulled in tension, detail of Fig. 1.

Fig. 3. Detail of necking development (on the left) and of the progressive formation of multiple necking in polypropylene (PP) thin-walled tubes subject to tension.

Fig. 4. Evidence of higher-order bifurcation modes in the necking of polypropylene (PP) thin-walled tubes under tension. Both trefoil and fourth-foiled modes have usually been observed, while, rarely, a fifth-foiled mode has also been found.

Fig. 5. Cross-sections of PP tubes under tension, showing: (a) the undeformed cross-section; (b) necking with uniform thinning; (c) necking involving a higher-order trefoil mode.

Fig. 6. Bifurcation upper envelopes for the critical stretch λ_z of an axially-compressed thin-walled cylinder (geometrical ratios r_e/r_i = 1.01, 1.02, 1.06) made up of a Mooney–Rivlin incompressible material with β = μ₂/μ₁ = −0.1. The curves corresponding to different values of the circumferential wave-number n and the relevant bifurcation modes (plotted on the cross-section of the shell) are indicated with the symbol . All the bifurcations here occur in compression, tensile bifurcations were not detected indeed.

Fig. 7. Bifurcation envelopes for the critical stretch λ_z of an axially-loaded thin-walled cylinder (geometrical ratios r_e/r_i = 1.01, 1.02, and 1.06) made up of a J₂-deformation theory incompressible material with exponent N = 0.1. The curves corresponding to different values of the circumferential wave-number n and the relevant bifurcation modes (plotted on the cross-section of the shell) are indicated with the symbol . Bifurcations here occur both in compression and tension. The only modes differing in tension and compression are necking and bulging, corresponding to n = 0.

Fig. 8. Bifurcation lower envelopes for the critical stretch λ_z of a moderately thin-walled cylinder (geometrical ratio r_e/r_i = 1.10), made of a J₂-deformation theory incompressible material with exponent N = 0.1 and subject to tension. The solid and dashed lines represent the predictions according to the 3d-exact analysis and the current Flügge 2d-approach, respectively, for different values of the circumferential wave-number n corresponding to the different bifurcation modes indicated.

Fig. 9. Bi-logarithmic representation (two different vertical scales are used) of the lower envelopes of the dimensionless load, (for the J₂-deformation theory material with N = 0.1) and p^MR_z (for the Mooney–Rivlin material with β = −0.1), vs. π/η, for the axially-compressed thin-walled cylinder with r_e/r_i = 1.01. For moderate values of π/η, the presence of a horizontal flat portion of the curve (highlighted as a red dashed line), corresponding to longitudinal wrinkling and leading to eqn (7.5), is evident for the Mooney–Rivlin material (and also for the neo–Hookean, not reported as almost superimposed to the Mooney–Rivlin material), but absent for the J₂-material.

Fig. 10. Nominal stress vs. conventional strain data for tensile tests on polypropylene (PP) thin-walled tubes (6.5 mm initial diameter, 0.18 mm thickness, 205 mm length). With a couple of exceptions, the samples were brought up to a conventional strain of approximately 5 where the test was terminated before failure. Three different gripping devices have been tested and the relevant experimental data are reported using the same colour. The ‘radial clamp’ was designed by us and is shown in Fig. 11.

Fig. 11. The experimental set-up for tensile tests on polypropylene (PP) thin-walled tubes. It is based on an electromechanical testing machine (Messphysik Midi 10). The ‘radial clamp’ device is shown on the right.

Fig. 12. Photographs taken after the failure of metallic tubes subject to a tensile test. From the upper to the lower side: copper and aluminium tubes (R_i = 6 mm, and R_e/R_i = 1.2) and two steel tubes (R_i = 6 mm, R_e/R_i = 1.25, and R_i = 8 mm, R_e/R_i = 1.23). While the steel tubes show an initial development of necking, the latter is not observed in neither copper nor aluminium tubes. Multiple necking and development of higher modes were not found. These metallic samples behaved completely differently from the PP tubes.

Fig. 13. Upper part: Nominal stress vs. conventional strain from a tensile test on a polypropylene (PP) thin-walled tube. Through ‘radial clamps’, the sample was brought before failure up to the conventional strain of 5. The final thickness was 0.06 mm. Lower part: nucleation and development of multiple necking. Although hardly visible in the photographs, higher-order modes were observed.