Using torsional wave elastography to evaluate spring pot parameters in skin tumor mimicking phantoms

Abstract

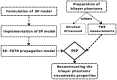
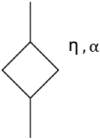
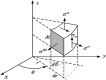
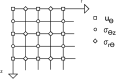
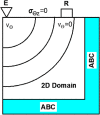
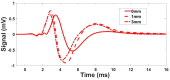
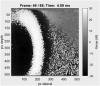
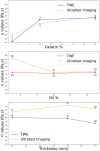
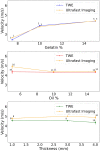
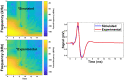
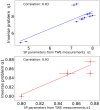
Estimating the tissue parameters of skin tumors is crucial for diagnosis and effective therapy in dermatology and related fields. However, identifying the most sensitive biomarkers require an optimal rheological model for simulating skin behavior this remains an ongoing research endeavor. Additionally, the multi-layered structure of the skin introduces further complexity to this task. In order to surmount these challenges, an inverse problem methodology, in conjunction with signal analysis techniques, is being employed. In this study, a fractional rheological model is presented to enhance the precision of skin tissue parameter estimation from the acquired signal from torsional wave elastography technique (TWE) on skin tumor-mimicking phantoms for lab validation and the estimation of the thickness of the cancerous layer. An exhaustive analysis of the spring-pot model (SP) solved by the finite difference time domain (FDTD) is conducted. The results of experiments performed using a TWE probe designed and prototyped in the laboratory were validated against ultrafast imaging carried out by the Verasonics Research System. Twelve tissue-mimicking phantoms, which precisely simulated the characteristics of skin tissue, were prepared for our experimental setting. The experimental data from these bi-layer phantoms were measured using a TWE probe, and the parameters of the skin tissue were estimated using inverse problem-solving. The agreement between the two datasets was evaluated by comparing the experimental data obtained from the TWE technique with simulated data from the SP- FDTD model using Pearson correlation, dynamic time warping (DTW), and time-frequency representation. Our findings show that the SP-FDTD model and TWE are capable of determining the mechanical properties of both layers in a bilayer phantom, using a single signal and an inverse problem approach. The ultrafast imaging and the validation of TWE results further demonstrate the robustness and reliability of our technology for a realistic range of phantoms. This fusion of the SP-FDTD model and TWE, as well as inverse problem-solving methods has the potential to have a considerable impact on diagnoses and treatments in dermatology and related fields.

Figure 1

Validation flowchart for the spring-pot viscoelastic model.

Figure 2

Spring pot model configuration.

Figure 3

Illustration of an infinitesimal element in cylindrical coordinates with stress components. This diagram depicts a differential element positioned within a cylindrical coordinate system $(r,\theta ,z)$ showing the normal and shear stress components $({\sigma }_{\mathit{rr}},{\sigma }_{\theta \theta },{\sigma }_{\mathit{zz}})$ acting on its faces. The element’s orientation demonstrates the relationship between the stresses and the coordinates, essential for analyzing stress in cylindrical bodies under load.

Figure 4

Grid discretization with staggered rows and columns indicating the locations of variables. displacement ($u_{\theta }$) and stresses (${\sigma }_{\theta z}$ ,${\sigma }_{r\theta }$).

Figure 5

The spatial distribution of the model boundary conditions. A two-dimensional domain is bordered by absorbing boundary conditions, excitation, reception ($v_{\theta }$ = 0), and free surface conditions.

Figure 6

The first scenario involves healthy tissue by itself, whereas the second case involves healthy tissue with a tumor of varying thicknesses.

Figure 7

Navigating the phantom process: a visual roadmap.

Figure 8

Experimental Setup for Torsional Wave Elastography. This photograph illustrates the experimental configuration, showcasing the phantom material placed beneath the torsional wave sensor. The setup includes the hardware for wave generation and reception, connected to a laptop running analytical software, which displays a typical waveform acquired during testing.

Figure 9

Imaging experimental setup. This figure shows the setup used for ultrafast imaging, with key components such as the transducer, phantom material, and the imaging system’s control unit highlighted. The setup is positioned to capture high-resolution images of shear wave propagation in the phantom.

Figure 10

Examples of experimental signals at 500 Hz with varying first layer thickness for phantoms 1 and 2.

Figure 11

Using the Verasonic’s vantage system, the image depicts the propagation of torsion waves inside a phantom.

Figure 12

Effect of gelatin, oil percentages, and thickness on $\eta$1 in the phantoms for the two techniques, torsion probe and ultrafast imaging approach (Numbers on points represent the Phantoms).

Figure 13

Effect of gelatin, oil percentages and thickness on torsional wave velocity in the phantoms for the two techniques, TWE and ultrafast imaging approach (numbers on points represent the phantoms).

Figure 14

An example of fitting experimental and simulated signals using the spring-pot model in the time domain for Phantom 1.

Figure 15

The correlation between the SP parameters reconstruction from TWE measurements for the single-layer phantom, which uses Eqs. (1) and (2), and the inverse problem method for reconstructing the parameters.