Bridging pharmacology and neural networks: A deep dive into neural ordinary differential equations
- PMID: 38992975
- PMCID: PMC11330178
- DOI: 10.1002/psp4.13149
Bridging pharmacology and neural networks: A deep dive into neural ordinary differential equations
Abstract
The advent of machine learning has led to innovative approaches in dealing with clinical data. Among these, Neural Ordinary Differential Equations (Neural ODEs), hybrid models merging mechanistic with deep learning models have shown promise in accurately modeling continuous dynamical systems. Although initial applications of Neural ODEs in the field of model-informed drug development and clinical pharmacology are becoming evident, applying these models to actual clinical trial datasets-characterized by sparse and irregularly timed measurements-poses several challenges. Traditional models often have limitations with sparse data, highlighting the urgent need to address this issue, potentially through the use of assumptions. This review examines the fundamentals of Neural ODEs, their ability to handle sparse and irregular data, and their applications in model-informed drug development.
© 2024 The Authors. CPT: Pharmacometrics & Systems Pharmacology published by Wiley Periodicals LLC on behalf of American Society for Clinical Pharmacology and Therapeutics.
Conflict of interest statement
Idris Bachali Losada is an employee of Randstad and contributed as a paid contractor for the Merck Quantitative Pharmacology, Ares Trading SA (an affiliate of Merck KGaA, Darmstadt, Germany), Lausanne, Switzerland. Nadia Terranova is an employee of Merck Quantitative Pharmacology, Ares Trading SA (an affiliate of Merck KGaA, Darmstadt, Germany), Lausanne, Switzerland.
Figures
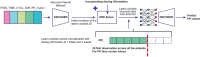
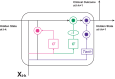
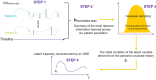
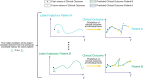
References
-
- Tornøe CW, Agersø H, Jonsson EN, Madsen H, Nielsen HA. Non‐linear mixed‐effects pharmacokinetic/pharmacodynamic modelling in NLME using differential equations. Comput Methods Prog Biomed. 2004;76(1):31‐40. - PubMed
-
- Chen RTQ, Rubanova Y, Betterncourt J, Duvenaud D. Neural ordinary differential equations. NeurIPS. 2018;31. 10.48550/arXiv.1806.07366 - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

