Sedimentation of a Charged Soft Sphere within a Charged Spherical Cavity
- PMID: 38999039
- PMCID: PMC11242989
- DOI: 10.3390/molecules29133087
Sedimentation of a Charged Soft Sphere within a Charged Spherical Cavity
Abstract
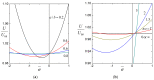
The sedimentation of a soft particle composed of an uncharged hard sphere core and a charged porous surface layer inside a concentric charged spherical cavity full of a symmetric electrolyte solution is analyzed in a quasi-steady state. By using a regular perturbation method with small fixed charge densities of the soft sphere and cavity wall, a set of linearized electrokinetic equations relevant to the fluid velocity field, electrical potential profile, and ionic electrochemical potential energy distributions are solved. A closed-form formula for the sedimentation velocity of the soft sphere is obtained as a function of the ratios of core-to-particle radii, particle-to-cavity radii, particle radius-to-Debye screening length, and particle radius-to-porous layer permeation length. The existence of the surface charge on the cavity wall increases the settling velocity of the charged soft sphere, principally because of the electroosmotic enhancement of fluid recirculation within the cavity induced by the sedimentation potential gradient. When the porous layer space charge and cavity wall surface charge have the same sign, the particle velocity is generally enhanced by the presence of the cavity. When these fixed charges have opposite signs, the particle velocity will be enhanced/reduced by the presence of the cavity if the wall surface charge density is sufficiently large/small relative to the porous layer space charge density in magnitude. The effect of the wall surface charge on the sedimentation of the soft sphere increases with decreases in the ratios of core-to-particle radii, particle-to-cavity radii, and particle radius-to-porous layer permeation length but is not a monotonic function of the ratio of particle radius-to-Debye length.
Keywords: boundary effect; charged cavity; charged soft particle; electrokinetics; sedimentation velocity.
Conflict of interest statement
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Figures





Similar articles
-
Sedimentation of a charged porous particle in a charged cavity.J Phys Chem B. 2013 Oct 10;117(40):12319-27. doi: 10.1021/jp407805x. Epub 2013 Sep 27. J Phys Chem B. 2013. PMID: 24041255
-
Sedimentation of a charged colloidal sphere in a charged cavity.J Chem Phys. 2011 Dec 7;135(21):214706. doi: 10.1063/1.3663380. J Chem Phys. 2011. PMID: 22149810
-
Electrophoresis of a charged soft particle in a charged cavity with arbitrary double-layer thickness.J Phys Chem B. 2013 Aug 22;117(33):9757-67. doi: 10.1021/jp405357e. Epub 2013 Aug 13. J Phys Chem B. 2013. PMID: 23898800
-
Diffusiophoresis of a spherical soft particle in electrolyte gradients.J Phys Chem B. 2012 Jun 28;116(25):7575-89. doi: 10.1021/jp302836g. Epub 2012 Jun 14. J Phys Chem B. 2012. PMID: 22651802
-
Diffusiophoresis of a Charged Porous Particle in a Charged Cavity.J Phys Chem B. 2018 Oct 25;122(42):9803-9814. doi: 10.1021/acs.jpcb.8b06967. Epub 2018 Oct 16. J Phys Chem B. 2018. PMID: 30280902
References
-
- Adachi Y. Sedimentation and Electrophoresis of a Porous Floc and a Colloidal Particle Coated with Polyelectrolytes. Curr. Opin. Colloid Interface Sci. 2016;24:72–78. doi: 10.1016/j.cocis.2016.06.003. - DOI
-
- Satoh A. Sedimentation Behavior of Dispersions Composed of Large and Small Charged Colloidal Particles: Development of New Technology to Improve the Visibility of Small Lakes and Ponds. Environ. Eng. Sci. 2015;32:528–538. doi: 10.1089/ees.2014.0493. - DOI
-
- Booth F. Sedimentation Potential and Velocity of Solid Spherical Particles. J. Chem. Phys. 1954;22:1956–1968. doi: 10.1063/1.1739975. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

