This is a preprint.
Heuristic energy-based cyclic peptide design
- PMID: 39005429
- PMCID: PMC11244984
- DOI: 10.1101/2024.07.03.601955
Heuristic energy-based cyclic peptide design
Update in
-
Heuristic energy-based cyclic peptide design.PLoS Comput Biol. 2025 Apr 30;21(4):e1012290. doi: 10.1371/journal.pcbi.1012290. eCollection 2025 Apr. PLoS Comput Biol. 2025. PMID: 40305587 Free PMC article.
Abstract
Rational computational design is crucial to the pursuit of novel drugs and therapeutic agents. Meso-scale cyclic peptides, which consist of 7-40 amino acid residues, are of particular interest due to their conformational rigidity, binding specificity, degradation resistance, and potential cell permeability. Because there are few natural cyclic peptides, de novo design involving non-canonical amino acids is a potentially useful goal. Here, we develop an efficient pipeline (CyclicChamp) for cyclic peptide design. After converting the cyclic constraint into an error function, we employ a variant of simulated annealing to search for low-energy peptide backbones while maintaining peptide closure. Compared to the previous random sampling approach, which was capable of sampling conformations of cyclic peptides of up to 14 residues, our method both greatly accelerates the computation speed for sampling conformations of small macrocycles (ca. 7 residues), and addresses the high-dimensionality challenge that large macrocycle designs often encounter. As a result, CyclicChamp makes conformational sampling tractable for 15- to 24-residue cyclic peptides, thus permitting the design of macrocycles in this size range. Microsecond-length molecular dynamics simulations on the resulting 15, 20, and 24 amino acid cyclic designs identify designs with kinetic stability. To test their thermodynamic stability, we perform additional replica exchange molecular dynamics simulations and generate free energy surfaces. Three 15-residue designs, one 20-residue and one 24-residue design emerge as promising candidates.
Figures
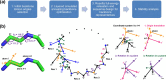
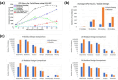
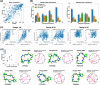






Similar articles
-
Heuristic energy-based cyclic peptide design.PLoS Comput Biol. 2025 Apr 30;21(4):e1012290. doi: 10.1371/journal.pcbi.1012290. eCollection 2025 Apr. PLoS Comput Biol. 2025. PMID: 40305587 Free PMC article.
-
Prediction, screening and characterization of novel bioactive tetrapeptide matrikines for skin rejuvenation.Br J Dermatol. 2024 Jun 20;191(1):92-106. doi: 10.1093/bjd/ljae061. Br J Dermatol. 2024. PMID: 38375775
-
Pharmacological and electronic cigarette interventions for smoking cessation in adults: component network meta-analyses.Cochrane Database Syst Rev. 2023 Sep 12;9(9):CD015226. doi: 10.1002/14651858.CD015226.pub2. Cochrane Database Syst Rev. 2023. PMID: 37696529 Free PMC article.
-
From Collagen Mimetics to Collagen Hybridization and Back.Acc Chem Res. 2024 Jun 18;57(12):1649-1657. doi: 10.1021/acs.accounts.3c00772. Epub 2024 May 25. Acc Chem Res. 2024. PMID: 38795029 Free PMC article.
-
AI-Driven Antimicrobial Peptide Discovery: Mining and Generation.Acc Chem Res. 2025 Jun 17;58(12):1831-1846. doi: 10.1021/acs.accounts.0c00594. Epub 2025 Jun 3. Acc Chem Res. 2025. PMID: 40459283 Free PMC article. Review.
References
-
- Zorzi A, Deyle K, Heinis C. Cyclic peptide therapeutics: past, present and future. Curr Opin Chem Biol. 2017;38:24–29. - PubMed
-
- Vinogradov AA, Yin Y, Suga H. Macrocyclic Peptides as Drug Candidates: Recent Progress and Remaining Challenges. J Am Chem Soc. 2019;141:4167–4181. - PubMed
-
- Mulligan V. The emerging role of computational design in peptide macrocycle drug discovery. Expert Opin Drug Discov. 2020;15:833–852. - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials
