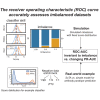
The receiver operating characteristic curve accurately assesses imbalanced datasets
- PMID: 39005487
- PMCID: PMC11240176
- DOI: 10.1016/j.patter.2024.100994
The receiver operating characteristic curve accurately assesses imbalanced datasets
Abstract
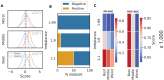
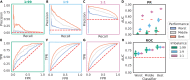
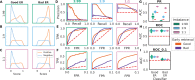
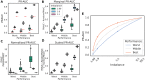
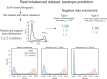
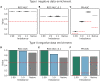
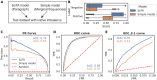
Many problems in biology require looking for a "needle in a haystack," corresponding to a binary classification where there are a few positives within a much larger set of negatives, which is referred to as a class imbalance. The receiver operating characteristic (ROC) curve and the associated area under the curve (AUC) have been reported as ill-suited to evaluate prediction performance on imbalanced problems where there is more interest in performance on the positive minority class, while the precision-recall (PR) curve is preferable. We show via simulation and a real case study that this is a misinterpretation of the difference between the ROC and PR spaces, showing that the ROC curve is robust to class imbalance, while the PR curve is highly sensitive to class imbalance. Furthermore, we show that class imbalance cannot be easily disentangled from classifier performance measured via PR-AUC.
Keywords: ROC curve; binary classification; imbalanced data; machine learning; performance metric; precision-recall.
© 2024 The Authors.
Conflict of interest statement
The authors declare no competing interests.
Figures


References
-
- Carter H., Chen S., Isik L., Tyekucheva S., Velculescu V.E., Kinzler K.W., Vogelstein B., Karchin R. Cancer-Specific High-Throughput Annotation of Somatic Mutations: Computational Prediction of Driver Missense Mutations. Cancer Res. 2009;69:6660–6667. doi: 10.1158/0008-5472.CAN-09-1133. - DOI - PMC - PubMed
-
- Sofaer H.R., Hoeting J.A., Jarnevich C.S. The area under the precision-recall curve as a performance metric for rare binary events. Methods Ecol. Evol. 2019;10:565–577. doi: 10.1111/2041-210X.13140. - DOI
-
- Thölke P., Mantilla-Ramos Y.-J., Abdelhedi H., Maschke C., Dehgan A., Harel Y., Kemtur A., Mekki Berrada L., Sahraoui M., Young T., et al. Class imbalance should not throw you off balance: Choosing the right classifiers and performance metrics for brain decoding with imbalanced data. Neuroimage. 2023;277 doi: 10.1016/j.neuroimage.2023.120253. - DOI - PubMed
Grants and funding
LinkOut - more resources
Full Text Sources
Research Materials

