Integrated Framework to Model Microstructure Evolution and Decipher the Microstructure-Property Relationship in Polymeric Porous Materials

Abstract

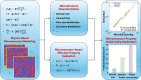
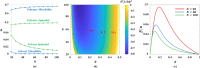
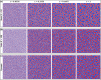
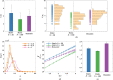
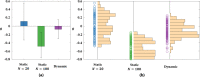
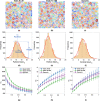
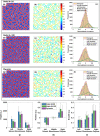
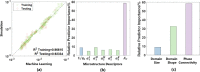
Unraveling the microstructure-property relationship is crucial for improving material performance and advancing the design of next-generation structural and functional materials. However, this is inherently challenging because it requires both the comprehensive quantification of microstructural features and the accurate assessment of corresponding properties. To meet these requirements, we developed an efficient and comprehensive integrated modeling framework, using polymeric porous materials as a representative model system. Our framework generates microstructures using a physics-based phase-field model, characterizes them using various average and localized microstructural features, and evaluates microstructure-aware properties, such as effective diffusivity, using an efficient Fourier-based perturbation numerical scheme. Additionally, the framework incorporates machine learning methods to decipher the intricate microstructure-property relationships. Our findings indicate that the connectivity of phase channels is the most critical microstructural descriptor for determining effective diffusivity, followed by the domain shape represented by curvature distribution, while the domain size has a minor impact. This comprehensive approach offers a novel framework for assessing microstructure-property relationships in polymer-based porous materials, paving the way for the development of advanced materials for diverse applications.

Keywords: dynamic polymerization kinetics; microstructure−property relationship; phase separation; polymeric porous materials; spinodal decomposition.

Figure 1

Integrated modeling framework to exploring the microstructure–property relationships of bicontinuous microstructures by incorporating physics-based microstructure modeling, microstructure characterization, microstructure-aware effective property evaluation, and microstructure–property relationship exploration.

Figure 2

(a) Equilibrium phase and spinodal composition as a function of degree of polymerization when χ = 1. The solvent and polymer miscibility lines represent the boundary for polymer-poor (solvent) and polymer-rich (polymer) single-phase region, i.e., the regions in between are the miscibility gap while the regions outside are single-phase solvent and polymer phases. (b) Thermodynamic instabilities in the N – ϕ space. (c) Composition-dependent mobility for different degrees of polymerization.

Figure 3

Phase-field simulation of the phase separation process at ϕ = 0.274 with (a) constant polymerization kinetics of N(t) = 20, (b) constant polymerization kinetics of N(t) = 100, and (c) dynamic polymerization kinetics with N(t) = 20 + 80t. Color legend: red for the polymer phase and blue for the solvent phase.

Figure 4

(a) Range and mean values of domain size. (b) Statistical distribution of domain size. (c) Circularly averaged structure factor S(q,t) as a function of distance from the center of the reciprocal space q for microstructure Static N = 20 at three different times. (d) Inverse of the first moment of structure factor as a function of time for three different polymerization kinetics and (e) coarsening coefficient of microstructures at t = 1 for different polymerization kinetics.

Figure 5

(a) Discreteness (θ) and (b) its statistical distribution of Static N = 20, Static N = 100, and Dynamic microstructures.

Figure 6

Pore size analysis for microstructures with different polymerization kinetics. (a–c) Maximal inscribed circles of microstructures at t = 1 in Figure 3. For clear presentation, only 80% of the circles are displayed. (d–f) Corresponding pore size distribution of panels (a–c). (g–i) Range and mean values for three Gaussian parameters, a₁ (peak height), a₂ (peak position), and a₃ (peak breadth) in eq 12 of Static N = 20, Static N = 100, and Dynamic microstructures.

Figure 7

Curvature distribution and distribution decomposition of Static N = 20, Static N = 100, and Dynamic microstructures. (a, d, g) Phase-field simulations at t = 1 from Figure 3. (b, e, h) Corresponding curvature maps. (c, f, i) Histograms of the curvature distributions as well as the three decomposed Gaussian peaks. (j–l) Statistics of the three decomposed Gaussian peaks of the curvature distributions of all of the simulations.

Figure 8

(a) Effective diffusivity and (b) statistical distributions among simulated microstructures for Static N = 20, Static N = 100, and Dynamic microstructures. The error bars in (a) represent the range of the data, rather than statistical error. Both y-axes are in log scale.

Figure 9

(a) Random forest model prediction compared with phase-field calculations of effective diffusivity. (b) Relative predictor importance from the random forest model in panel (a). (c) Aggregated relative predictor importance for three different descriptors: domain size, domain shape, and domain connectivity.

Figure 10

Schematic illustration of domain size evolution for static and dynamic polymerization kinetics. The symbol ≲ represents “slightly smaller than, approximately equal to”. It is worth noting that the parallel linear curves for the static N cases in this figure are strictly physical as they would all follow the Lifshitz–Slyozov–Wagner long-term coarsening kinetics with the coarsening coefficient n = 3. On the other hand, the curve for Dynamic N is schematic and its shape would depend on the polymerization kinetics.

Figure 11

(a) Different polymerization kinetics, (b) corresponding domain size evolution, and (c) discreteness values at t = 1. Note that only the mean discreteness and domain size values for Static N = 20, Static N = 100, and Dynamic microstructures are shown for comparison, titled “Static-Mean N = 20”, “Static-Mean N = 100”, and “Dynamic Linear-Mean”.

Figure 12

Microstructure and property comparison for two seemingly similar microstructures. (a, d) Are the original microstructures with the blue phase as solvent and the red phase as the polymer phase. (b, e) Shows the connected solvent domains from (a, e) under periodic boundary conditions. (c, f) Are the connected domains in the 3 × 3 image of (b, e) with a fixed boundary condition. The table in between shows the values for effective diffusivity (D_eff), discreteness (θ), area fraction of connected domains (A_C), and domain size (1/q₁).