Fractional order cancer model infection in human with CD8+ T cells and anti-PD-L1 therapy: simulations and control strategy

Abstract

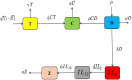
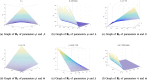
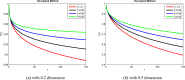
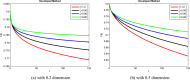
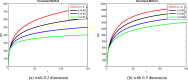
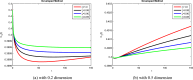
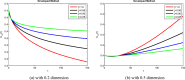
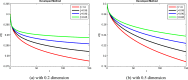
In order to comprehend the dynamics of disease propagation within a society, mathematical formulations are essential. The purpose of this work is to investigate the diagnosis and treatment of lung cancer in persons with weakened immune systems by introducing cytokines ( $I{L}_2\&I{L}_{12}$ ) and anti-PD-L1 inhibitors. To find the stable position of a recently built system TCD $I{L}_{2}I{L}_{12}$ Z, a qualitative and quantitative analysis are taken under sensitive parameters. Reliable bounded findings are ensured by examining the generated system's boundedness, positivity, uniqueness, and local stability analysis, which are the crucial characteristics of epidemic models. The positive solutions with linear growth are shown to be verified by the global derivative, and the rate of impact across every sub-compartment is determined using Lipschitz criteria. Using Lyapunov functions with first derivative, the system's global stability is examined in order to evaluate the combined effects of cytokines and anti-PD-L1 inhibitors on people with weakened immune systems. Reliability is achieved by employing the Mittag-Leffler kernel in conjunction with a fractal-fractional operator because FFO provide continuous monitoring of lung cancer in multidimensional way. The symptomatic and asymptomatic effects of lung cancer sickness are investigated using simulations in order to validate the relationship between anti-PD-L1 inhibitors, cytokines, and the immune system. Also, identify the actual state of lung cancer control with early diagnosis and therapy by introducing cytokines and anti-PD-L1 inhibitors, which aid in the patients' production of anti-cancer cells. Investigating the transmission of illness and creating control methods based on our validated results will both benefit from this kind of research.

Keywords: Boundedness; Cancer model; Fractional operator; Global derivative; Mathematical modeling; Stability analysis.

Figure 1

The model formulation is shown in the flow chart.

Figure 2

Reproductive number behavior for the newly developed system under different parameter effects.

Figure 3

Simulation of T(t) using FFM with different dimensions.

Figure 4

Simulation of C(t) using FFM with different dimensions.

Figure 5

Simulation of D(t) using FFM with different dimensions.

Figure 6

Simulation of $I{L}_2(t)$ using FFM with different dimensions.

Figure 7

Simulation of $I{L}_{12}(t)$ using FFM with different dimensions.

Figure 8

Simulation of Z(t) using FFM with different dimensions.