The use of constrained methods to analyze the molecular reactivity and to define a new type of pseudo atoms

Abstract

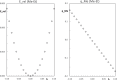
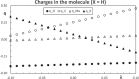
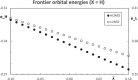
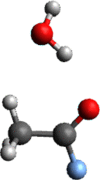
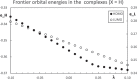
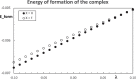
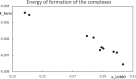
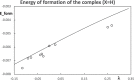
Context: Constrained methods in electronic structure methodologies add terms to the variational equations and generate solutions that represent distorted electronic distributions. In some cases, the new solutions can be used to study the chemical reactivity of parts of the molecule. Additionally, this contribution presents the use of population constraints to define pseudo atoms in a molecule. The effects of the pseudo atom on the molecular properties are analyzed. The pseudo atoms are used to simulate the inductive effect of the substituent in a group of carbonyl molecules and their effect on the stability of the complexes between these organic species and one molecule of water. A discussion on the assumptions involved in the present definition of pseudo atoms is also included.

Method: The constrained RHF computations are done in a modified Hartree-Fock code for Gaussian basis sets. The selected basis set is STO-6 G.

Keywords: Chemical reactivity; Constrained methods; Electronic structure; Hydrogen bonds; Pseudo atoms.

Fig. 1

Change of the constrained molecular energy of the propane molecule ${\text{CH}}_3{\text{CH}}_2{\text{CH}}_3$, relative to the unconstrained molecule (left side), and charge of the constrained methyl group as a function of the Lagrange multiplier $\lambda$ (right side). All quantities are in atomic units

Fig. 2

Structure of the carbonyl compounds $\text{Me-C(=O)-R}$, where the substituent $\text{R}$ is represented by a blue sphere

Fig. 3

Computed charges of the carbonyl molecule using $\text{X=H}$ as the pseudo atom

Fig. 4

Computed orbital energies of the carbonyl molecule using $\text{X=H}$ as the pseudo atom. All values are in atomic units

Fig. 5

Structure of the hydrogen bond stabilized complex between a carbonyl compound $\text{Me-C(=O)-R}$ and one water molecule. Here, the substituent $\text{R}$ is represented by a blue sphere

Fig. 6

Computed charges within the hydrogen bond stabilized complexes $\text{Me-C(-X)=O}\cdots \text{w}$ using the $\text{X=H}$ as the pseudo atom

Fig. 7

Computed orbital energies for the hydrogen bond stabilized complexes $\text{Me-C(-X)=O}\cdots \text{w}$ using the $\text{X=H}$ as the pseudo atom. All values are in atomic units

Fig. 8

Computed energies of formation of the hydrogen bond stabilized complexes $\text{Me-C(-X)=O}\cdots \text{w}$ using the $\text{X=H,F}$ as the pseudo atom. All values are in atomic units

Fig. 9

Relation between the estimated energies of formation of the hydrogen bond stabilized complexes $\text{Me-C(-X)=O}\cdots \text{w}$ and the LUMO eigenvalue of the carbonyl molecule. All values are in atomic units

Fig. 10

Predicted energies of formation of the hydrogen bond stabilized complexes $\text{Me-C(-X)=O}\cdots \text{w}$ using the $\text{X=H}$ as the pseudo atom (line) and computed values (circles). All values are in atomic units

Fig. 11

Predicted energies of formation of the hydrogen bond stabilized complexes $\text{Me-C(-X)=O}\cdots \text{w}$ using the $\text{X=F}$ as the pseudo atom (line) and computed values (circles). All values are in atomic units