Haplotype-aware sequence alignment to pangenome graphs

Abstract

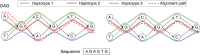
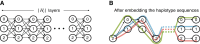
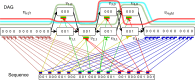
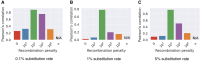
Modern pangenome graphs are built using haplotype-resolved genome assemblies. When mapping reads to a pangenome graph, prioritizing alignments that are consistent with the known haplotypes improves genotyping accuracy. However, the existing rigorous formulations for colinear chaining and alignment problems do not consider the haplotype paths in a pangenome graph. This often leads to spurious read alignments to those paths that are unlikely recombinations of the known haplotypes. In this paper, we develop novel formulations and algorithms for sequence-to-graph alignment and chaining problems. Inspired by the genotype imputation models, we assume that a query sequence is an imperfect mosaic of reference haplotypes. Accordingly, we introduce a recombination penalty in the scoring functions for each haplotype switch. First, we solve haplotype-aware sequence-to-graph alignment in [Formula: see text] time, where Q is the query sequence, E is the set of edges, and H is the set of haplotypes represented in the graph. To complement our solution, we prove that an algorithm significantly faster than [Formula: see text] is impossible under the strong exponential time hypothesis (SETH). Second, we propose a haplotype-aware chaining algorithm that runs in [Formula: see text] time after graph preprocessing, where N is the count of input anchors. We then establish that a chaining algorithm significantly faster than [Formula: see text] is impossible under SETH. As a proof-of-concept, we implemented our chaining algorithm in the Minichain aligner. By aligning sequences sampled from the human major histocompatibility complex (MHC) to a pangenome graph of 60 MHC haplotypes, we demonstrate that our algorithm achieves better consistency with ground-truth recombinations compared with a haplotype-agnostic algorithm.

Figure 1.

An example of an acyclic pangenome graph built using three haplotypes. The left figure shows the optimal alignment of the query sequence to the DAG with minimum edit distance. Accordingly, the edit distance is zero, and the count of recombinations is two. Next, suppose that we use recombination penalty −5 (formally defined in Methods). The right figure shows the new optimal alignment, where there is no recombination because the alignment path is consistent with haplotype 2.

Figure 2.

An illustration of the pangenome DAG used in the reduction proof of Lemma 3. An initial version of the DAG (A) and the changes made after addition of all the haplotype paths (B).

Figure 3.

An example that shows anchors (in red) between a query sequence and a pangenome DAG. The DAG comprises three haplotype sequences, H₁, H₂, H₃. In this example, the ordered sequence of pairs [(2, 1), (4, 1), (5, 1), (9, 1), (10, 1), (13, 3), (14, 3)] forms a chain, and the corresponding anchors are highlighted using blue markers. This chain includes a single recombination.

Figure 4.

Reduction from OV problem with sets A = {0110, 1100, 1101} and B = {1010, 1001, 1011}.

Figure 5.

An example to illustrate simulation of a query sequence as a mosaic of reference haplotypes. In this example, l = 19.

Figure 6.

Pearson's correlation between the number of recombinations in Minichain's output chain and the true count. We evaluated the performance with substitution rates 0.1% (A), 1% (B), and 5% (C) and different recombination penalties.

Figure 7.

Box plots show the levels of consistency between the haplotype recombination pairs in Minichain's output chain and the ground truth using three different sets of simulated MHC sequences with substitution rates 0.1% (A), 1% (B), and 5% (C). We tested using different recombination penalties. Each red dot in the plots corresponds to a query sequence. The median values are highlighted in green.