Large-scale photonic network with squeezed vacuum states for molecular vibronic spectroscopy
- PMID: 39025843
- PMCID: PMC11258230
- DOI: 10.1038/s41467-024-50060-2
Large-scale photonic network with squeezed vacuum states for molecular vibronic spectroscopy
Abstract
Although molecular vibronic spectra generation is pivotal for chemical analysis, tackling such exponentially complex tasks on classical computers remains inefficient. Quantum simulation, though theoretically promising, faces technological challenges in experimentally extracting vibronic spectra for molecules with multiple modes. Here, we propose a nontrivial algorithm to generate the vibronic spectra using states with zero displacements (squeezed vacuum states) coupled to a linear optical network, offering ease of experimental implementation. We also fabricate an integrated quantum photonic microprocessor chip as a versatile simulation platform containing 16 modes of single-mode squeezed vacuum states and a fully programmable interferometer network. Molecular vibronic spectra of formic acid and thymine under the Condon approximation are simulated using the quantum microprocessor chip with high reconstructed fidelity ( > 92%). Furthermore, vibronic spectra of naphthalene, phenanthrene, and benzene under the non-Condon approximation are also experimentally simulated. Such demonstrations could pave the way for solving complicated quantum chemistry problems involving vibronic spectra and computational tasks beyond the reach of classical computers.
© 2024. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures
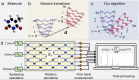
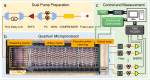
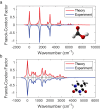

References
-
- Sharp TE, Rosenstock HM. Franck–Condon factors for polyatomic molecules. J. Chem. Phys. 1964;41:3453–3463. doi: 10.1063/1.1725748. - DOI
-
- Bromley, T. R., Arrazola, J. M. & Jahangiri, S. Applications of near-term photonic quantum computers: software and algorithms. Quantum Sci. Technol.5, 034010 2020.
-
- Doktorov EV, Malkin IA, Man’ko VI. Dynamical symmetry of vibronic transitions in polyatomic molecules and the Franck–Condon principle. J. Mol. Spectrosc., 1977;64:302–326. doi: 10.1016/0022-2852(77)90269-7. - DOI
-
- Malmqvist P-Å, Forsberg N. Franck–Condon factors for multidimensional harmonic oscillators. Chem. Phys. 1998;228:227–240. doi: 10.1016/S0301-0104(97)00347-9. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

