Streamflow Prediction Using Complex Networks

Abstract

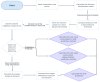
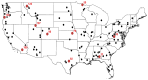
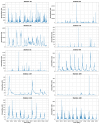
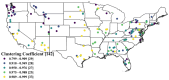
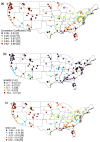
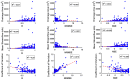
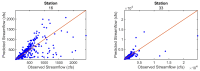
The reliable prediction of streamflow is crucial for various water resources, environmental, and ecosystem applications. The current study employs a complex networks-based approach for the prediction of streamflow. The approach consists of three major steps: (1) the formation of a network using streamflow time series; (2) the calculation of the clustering coefficient (CC) as a network measure; and (3) the use of a clustering coefficient-based nearest neighbor search procedure for streamflow prediction. For network construction, each timestep is considered as a node and the existence of link between any node pair is identified based on the difference (distance) between the streamflow values of the nodes. Different distance threshold values are used to identify the critical distance threshold to form the network. The complex networks-based approach is implemented for the prediction of daily streamflow at 142 stations in the contiguous United States. The prediction accuracy is quantified using three statistical measures: correlation coefficient (R), normalized root mean square error (NRMSE), and Nash-Sutcliffe efficiency (NSE). The influence of the number of neighbors on the prediction accuracy is also investigated. The results, obtained with the critical distance threshold, reveal that the clustering coefficients for the 142 stations range from 0.799 to 0.999. Overall, the prediction approach yields reasonably good results for all 142 stations, with R values ranging from 0.05 to 0.99, NRMSE values ranging from 0.1 to 12.3, and the NSE values ranging from -0.89 to 0.99. An attempt is also made to examine the relationship between prediction accuracy and the catchment characteristics/streamflow statistical properties (drainage area, mean flow, coefficient of variation of flow). The results suggest that the prediction accuracy does not have much of a relationship with the drainage area and the mean streamflow values, but with the coefficient of variation of flow. The outcomes from this study are certainly promising regarding the application of complex networks-based concepts for the prediction of streamflow (and other hydrologic) time series.

Keywords: clustering coefficient; coefficient of variation; contiguous United States; distance threshold; nearest neighbor approach; network theory.

Figure A1

Flowchart for the complex network-based prediction approach used in this study.

Figure 1

Geographical locations of the 142 streamflow gauging stations across the contiguous United States considered in this study. The ten stations marked in red are selected for the purpose of the illustration of results and discussion.

Figure 2

Time series plots of streamflow from ten selected stations in the United States.

Figure 3

Links for the first node (day 1) in the streamflow network of Station 16 (USGS Station #2011400, Jackson River near Bacova, VA).

Figure 4

Clustering coefficient values of 142 streamflow networks across the United States. The numbers within the brackets represent the count of stations within that range of values.

Figure 5

Variation in prediction accuracy with respect to the different number of neighbors for ten the selected stations: (a) R; (b) NRMSE; and (c) NSE.

Figure 6

(a–c) Values of R, NRMSE, and NSE obtained for 142 stations across the United States. The numbers within the brackets represent the count of stations within that range of values.

Figure 7

Scatter plot showing the relationship between prediction accuracies and both the statistical characteristics of streamflow data and its catchment characteristics.

Figure 8

Scatter plot between observed and predicted streamflow for 10 selected stations.

Figure 8

Scatter plot between observed and predicted streamflow for 10 selected stations.