Non-equilibrium transport in polymer mixed ionic-electronic conductors at ultrahigh charge densities

Abstract

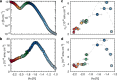
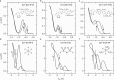
Conducting polymers are mixed ionic-electronic conductors that are emerging candidates for neuromorphic computing, bioelectronics and thermoelectrics. However, fundamental aspects of their many-body correlated electron-ion transport physics remain poorly understood. Here we show that in p-type organic electrochemical transistors it is possible to remove all of the electrons from the valence band and even access deeper bands without degradation. By adding a second, field-effect gate electrode, additional electrons or holes can be injected at set doping states. Under conditions where the counterions are unable to equilibrate in response to field-induced changes in the electronic carrier density, we observe surprising, non-equilibrium transport signatures that provide unique insights into the interaction-driven formation of a frozen, soft Coulomb gap in the density of states. Our work identifies new strategies for substantially enhancing the transport properties of conducting polymers by exploiting non-equilibrium states in the coupled system of electronic charges and counterions.

Fig. 1. Observation of deep band-filling behaviour in IDT-BT OECTs.

a, Device structure. b, Transfer curve for an IDT-BT OECT, taken at room temperature with a drain voltage V_D of −0.1 V. The dashed grey line indicates the gate leakage current and the arrow indicates the voltage sweep direction. n represents the number of dopant ion per polymer repeat unit. c, Chemical structures of IDT-BT, BMP TFSI and PVDF-HFP. n, x  and y represent the number of IDT-BT, PVDF, and HFP repeat units, respectively. d, Temperature dependence of the Seebeck coefficient S of IDT-BT at various doping levels. These doping levels are shown schematically on an OECT transfer curve in the inset. e, Seebeck–conductivity plot at 200 K for the data shown in d. The arrows denote the direction of increasing doping level for a given regime. In d and e, the data are presented as the mean Seebeck coefficient ± standard error of the mean, originating from fitting uncertainties of the on-chip thermometer calibration and the thermovoltage versus temperature difference plots. Lines are included as a guide to the eye.

Fig. 2. Non-equilibrium transport signatures in IDT-BT double-gated transistors.

a, Schematic of the double-gated transistor experiment. b, Electrical conductivity at V_FG = 0 V of various doping states at 160 K. Insets show field-effect transfer curves for six representative doping states at 160 K. As the film conductivity changes by orders of magnitude as the doping level is increased, the drain current is normalized as (I_D(V_FG) − I_min)/I_min, where I_min is the minimum current in the field-effect transfer curve of the corresponding doping state. For each inset the maximum field-effect modulation is indicated as a percentage value. At the conductivity peak, the current decreases when changing V_IG but increases when changing V_FG. c, Field-effect transfer curves for an ex-situ-doped IDT-BT device between 300 and 220 K, exhibiting non-linear behaviour at low temperatures. The transfer curves are vertically shifted for clarity. The magnitude of the arrow represents 0.4 μS. The inset shows a schematic of the decomposition of the 220 K transfer curve into a linear antisymmetric component and a symmetric component. d, ¹⁹F nuclear spin–lattice relaxation time (T₁) and spin–spin relaxation time (T₂) versus temperature (T) obtained from ¹⁹F NMR saturation recovery and spin-echo delay experiments of IDT-BT doped with TFSI. The inset shows the extracted correlation times (τ_c) from a two-component fit described in Supplementary Note 7.

Fig. 3. Theoretical modelling of non-equilibrium transport.

a–c, Transfer curves calculated in and out of equilibrium for systems at electrochemical doping levels of 0.4 (a), 1.2 (b) and 1.6 ions per monomer (c). The effect of the field-effect gate bias is modelled as a relative change in the charge density, Δn/n₀, where n₀ is the number of electrons in a full band. Data are presented as the mean of 400 realizations ± standard error of the mean. d, DOS in the absence of field-effect gating, with and without ionic relaxation at a doping level of 1.2 ions per monomer. e-e interaction, electron–electron interaction. e, DOS around E_F for positive and negative gate bias under out-of-equilibrium conditions. The arrows mark the Fermi level for different Δn/n₀. f,g, Relative variation of the DOS at E_F (f) and relative variation of the participation ratio L(E_F) (g), measuring the degree of delocalization of the carriers. h, Schematic of the free energy landscape in equilibrium (left) and out of equilibrium (right). Equilibrium cases refer to mobile ion and/or zero-gate bias conditions, while non-equilibrium refers to the case of frozen ions with non-zero gate bias. The contributions of disorder and e-e interaction (top), ionic relaxation (middle) and their sum (bottom) are shown schematically. In the non-equilibrium condition the gate bias alters the electronic energy landscape (red arrow), but the ionic relaxation contribution remains unchanged. This leads to a smaller energy barrier (green arrow) to escape from the energy minimum.

Fig. 4. Spectroscopic evidence for enhanced delocalization of non-equilibrium states.

a,b, CMS spectra of an IDT-BT:TFSI film doped to Regime I at 270 K (a) and 190 K (b). The bottom left insets show the transfer curves at each temperature. The symbols show the experimental data, and the solid lines are fits from the decomposed symmetric and antisymmetric component spectra as described in the text. OD, optical density. c, Antisymmetric (top) and symmetric (bottom) component spectra used to fit the data. The antisymmetric component (blue line, 270 K data shown) matches closely the OECT moving difference spectrum (green line) calculated from the data in Extended Data Fig. 4. The symmetric component (red line, difference between 190 K and 270 K data shown) is nearly independent of the doping level and reflects an increase in carrier delocalization upon field-effect gating below the ionic glass transition temperature.

Fig. 5. Enhancement of the Seebeck coefficient due to the frozen Coulomb gap.

a,b, Field-effect transfer curve (V_D = −0.1 V) of a highly doped IDT-BT device measured at 190 K (in Regime III, see inset) (a), where changes in the magnitude of the Seebeck coefficient across the gap are indicated on the transfer curve, as inferred from thermovoltage measurements at various field-effect gate voltages (b).

Extended Data Fig. 1. Carrier density analysis based on the comparison of the abundance of sulfur atoms in the polymer backbone and the dopant ion.

Sulfur 2p peak in the X-ray photoemission spectra of (a) PBTTT, (b) DPP-BTz, and (c) IDT-BT at various doping levels. The dopant ion peak appears at higher binding energies, denoted as S_TFSI. The number of dopant ions per polymer repeat unit n, determined from integration areas, is indicated on each doped spectrum. Close to the conductivity peak we estimate a 1:1 ratio of TFSI ions to polymer repeat units for all three materials, consistent with half-band filling. The doping level in the valley of IDT-BT is approximately 1.5 ions per repeat unit, indicative of some overlap between HOMO and HOMO-1 bands. Regime III should correspond to carrier densities of up to 3 ions per repeat unit, but direct measurements of these highest doped samples were challenging due to sample dedoping under ultrahigh vacuum. Fitting and analysis details are provided in Supplementary Note 3.4.

Extended Data Fig. 2. Doping induced changes in the frontier energy levels of conjugated polymers as inferred from ultraviolet photoemission spectroscopy (UPS).

UPS spectra of (a) PBTTT, (b) DPP-BTz, and (c) IDT-BT at various doping levels. Top right insets show a detailed view of the Fermi level, highlighting the presence of a finite filled DOS indicative of metallic characteristics in the highly doped samples. In DPP-BTz the HOMO-derived band is completely emptied in the insulating state of Regime II. More detailed discussion is provided in Supplementary Note 3.3.

Extended Data Fig. 3. Multiple redox features in DPP-BTz and IDT-BT.

Cyclic voltammogram (bottom panels, sweep rate 10 mV s⁻¹ for PBTTT and DPP-BTz, 2 mV s⁻¹ for IDT-BT) and the corresponding conductivity at various doping stages (top panels) for (a) PBTTT, (b) DPP-BTz, and (c) IDT-BT. In PBTTT, we see only one redox feature at the onset of its Regime I. In DPP-BTz, we see two redox features — one at the onset of Regime I, and another within Regime II. In IDT-BT, we see three redox features corresponding to the three transport regimes — two close together at 0.7 V vs Fc/Fc⁺ coinciding with the conductivity peak between Regimes I and II, and a third one at the onset of Regime III. The observation that the conductivity peak occurs between the first two redox waves — which each appear to be single-electron transfer events — is consistent with our picture of maximum conduction near half-band filling. Note that the voltage in cyclic voltammetry is applied to the polymer, such that the sign of the applied voltage is reversed relative to the OECT measurements.

Extended Data Fig. 4. In-situ optical spectroscopy of ion gated IDT-BT.

In-operando (a) UV-Vis-NIR and (b) FT-IR measurements of IDT-BT OECTs. UV-Vis-NIR spectra show absolute absorbance, FT-IR spectra show absorbance change from the off state (V_IG = 0 V). OD, optical density. In Regime I, the bleaching of the π − π^* band at 2 eV due to removal of charge from the HOMO band reaches completion exactly at the conductivity peak, consistent with the removal of one electron per repeat unit. The IR absorption similarly is maximized at the end of Regime I. In Regimes II and III, an isosbestic point appears in the IR spectrum near 0.3 eV, indicative of a one-to-one interconversion between polaronic species with fixed total concentration, that is the conversion of singly charged states into multiply charged states.

Extended Data Fig. 5. Electron spin resonance (ESR) spectroscopy of ion gated IDT-BT.

(a-b) ESR measurements of an IDT-BT OECT at 290 K: (a) device transfer curve and (b) total magnetic susceptibility. The decrease in total susceptibility at V_IG < −1.6 V is attributed to the onset of spin pairing; this reduction slows down beyond the valley in the conductivity, which could signal the onset of Regime III in some parts of the heterogeneous microstructure. (c-d) Paramagnetic susceptibility components extracted from temperature-dependent measurements: (c) Curie component of susceptibility and (d) Pauli component of susceptibility. Dashed lines are a guide for the eye showing the scaled total magnetic susceptibility trend. Gate voltages in (c,d) have been corrected for threshold voltage shifts during temperature sweeps; the corrected gate voltages are presented as the best fit values ± mean absolute error, where the best fit values are obtained by minimising their residuals. The Curie component dominates at low doping levels, whereas the Pauli component is dominant around the conductivity peak. The Curie component persists up to the most negative V_IG, which indicates that complete spin-pairing of these Curie spins is hindered, perhaps by strong on-site Coulombic repulsions or heterogeneity in the microstructure. The Pauli component drops considerably towards the conductivity valley, consistent with the interpretation of the Pauli susceptibility being a measure of the DOS at the Fermi level experienced by the metallic spins. See Supplementary Note 3.8 for an extended discussion of the physical interpretation and the gate voltage correction routine.

Extended Data Fig. 6. Other polymer/ion combinations allowing access to Regime III.

(a-c) OECT transfer curves of other polymers gated with TFSI: (a) indacenodithiophene-co-benzooxadiazole (IDT-BO), (b) indacenodithiophene-co-benzoselenadiazole (IDT-BS), and (c) indacenodithieno[3,2-b]thiophene-co-benzothiadiazole (IDTT-BT). (d-f) OECT transfer curves of IDT-BT gated with different ions: (d) hexafluorophosphate (PF₆), (e) bis(fluorosulfonyl)imide (FSI), and (f) tris(pentafluoroethyl) trifluorophosphate (FAP). Insets are the molecular structures of the corresponding polymers or ions. All transfer curves were taken at room temperature with V_D = −0.1 V. These results demonstrate that Regime III operation is not unique to IDT-BT gated with TFSI. The smallest of these anions, PF₆, shows a decreased electrochemical stability, leading to a strong reduction in peak current on the reverse scan.

Extended Data Fig. 7. Band filling in PBTTT and DPP-BTz.

(a) Molecular structures of PBTTT and DPP-BTz. (b) OECT transfer curves of typical PBTTT and DPP-BTz devices gated with BMP TFSI (room temperature, V_D = −0.1 V). In PBTTT a monotonic increase of conductivity with increasingly negative gate voltages is seen, suggesting that the device remains in Regime I throughout. Conversely in DPP-BTz a decrease of conductivity at high gate voltages is seen, suggesting a crossover to Regime II. (c) Temperature dependence of the Seebeck coefficient of PBTTT and DPP-BTz. Data are presented as the mean Seebeck coefficients ± standard error of the mean, originating from fitting uncertainties of the on-chip thermometer calibration and the thermovoltage versus temperature difference plots. The absence of n-type transition in PBTTT confirms that PBTTT remains in Regime I even at the highest doping levels (n ≈ 1) attainable in the present study. In DPP-BTz, a transition to n-type transport is observed beyond the conductivity peak, confirming the accessibility of Regime II in DPP-BTz.

Extended Data Fig. 8. DFT DOS and band structure calculations.

DFT band structure (left) and DOS (right) of (a) IDT-BT, (b) DPP-BTz, and (c) PBTTT along the polymer backbone direction Γ − X. Doping level n indicates the number of ions per repeat unit. In comparison to IDT-BT, DPP-BTz displays a relatively narrow HOMO (bandwidth = 0.55 eV), but a deeper HOMO-1 derived band edge which may contribute to the inaccessibility of Regime III. PBTTT shows a considerably broader HOMO (bandwidth = 1.22 eV) compared to DPP-BTz and IDT-BT, which likewise may contribute to the inaccessability of Regimes II and III (see further discussion in Supplementary Note 3). We stress that although the relative differences between the band structure and DOS derived from these calculations are instructive, they neglect important factors such as electron-ion interactions and microstructural disorder. Therefore, the DOS obtained here is not expected to be consistent to our experimental band filling data (Fig. 1 and Extended Data Fig. 7). GIWAXS data (Supplementary Note 4) suggest that structural changes upon doping, which are not captured in these DFT calculations, may be more relevant in explaining the inaccessability of Regime II in PBTTT.

Extended Data Fig. 9. Non-equilibrium transport signatures in double-gated PBTTT and DPP-BTz measurements.

Top panels show the electrical conductivities of (a) PBTTT and (b) DPP-BTz, at V_FG = 0 V for different doping states at 160 K, with insets showing field-effect transfer curves for several representative doping states and the percentage of maximum modulation in I_D. Bottom panels show the symmetric and anti-symmetric carrier mobilities, as defined in Supplementary Note 6.1. For DPP-BTz, the inset in the anti-symmetric mobility plot is a zoomed-in view for doping states 5, 6, and 7. In DPP-BTz we observe an ambipolar behaviour similar to IDT-BT. In PBTTT, the non-equilibrium transport manifests itself as a deviation from linearity in the field-effect transfer curves, which is evident in doping states 1 and 2 at 160 K, but becomes observable and more pronounced in all doping states at lower temperatures (Supplementary Note 6.4). These results demonstrate that our observation of non-equilibrium transport is general and extends to higher mobility polymers with room temperature conductivities of > 100 − 1, 000 S cm⁻¹.

Extended Data Fig. 10. Field-effect mobilities extracted from the symmetric and anti-symmetric components of the field-effect transfer characteristics of IDT-BT.

Measurements were performed at 160 K. The magnitude of the anti-symmetric field-effect mobilities are generally lower than the symmetric mobilities, for example 0.02 cm² V⁻¹ s⁻¹ (anti-symmetric) vs. 0.04 cm² V⁻¹ s⁻¹ (symmetric) for doping state 3, indicative of enhanced charge transport in the field-effect induced non-equilibrium states. Mobilities are extracted from the complete dataset shown in Fig. 2(b) and Supplementary Fig. 26.