Casimir Effect in MEMS: Materials, Geometries, and Metrologies-A Review
- PMID: 39063687
- PMCID: PMC11278474
- DOI: 10.3390/ma17143393
Casimir Effect in MEMS: Materials, Geometries, and Metrologies-A Review
Abstract
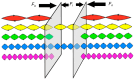
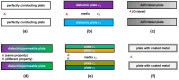
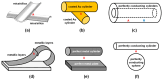
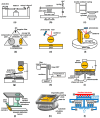
Casimir force densities, i.e., force per area, become very large if two solid material surfaces come closer together to each other than 10 nm. In most cases, the forces are attractive. In some cases, they can be repulsive depending on the solid materials and the fluid medium in between. This review provides an overview of experimental and theoretical studies that have been performed and focuses on four main aspects: (i) the combinations of different materials, (ii) the considered geometries, (iii) the applied experimental measurement methodologies and (iv) a novel self-assembly methodology based on Casimir forces. Briefly reviewed is also the influence of additional parameters such as temperature, conductivity, and surface roughness. The Casimir effect opens many application possibilities in microelectromechanical systems (MEMS) and nanoelectromechanical systems (NEMS), where an overview is also provided. The knowledge generation in this fascinating field requires interdisciplinary approaches to generate synergetic effects between technological fabrication metrology, theoretical simulations, the establishment of adequate models, artificial intelligence, and machine learning. Finally, multiple applications are addressed as a research roadmap.
Keywords: Casimir effect; Van-der-Waals force; attraction and repulsion; dispersion forces; nanocavities; retardation; self-assembly; solid–fluid interfaces; surface roughness.
Conflict of interest statement
The authors declare no conflict of interest.
Figures



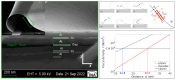
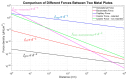

References
-
- Casimir H.B.G. On the attraction between two perfectly conducting plates. Proc. Kon. Ned. Akad. Wet. 1948;51:793–796.
-
- Casimir H.B.G., Polder D. The Influence of Retardation on the London-van der Waals Forces. Phys. Rev. 1948;73:360–372. doi: 10.1103/PhysRev.73.360. - DOI
-
- Israelachvili J.N., Tabor D. The measurement of van der Waals dispersion forces in the range 1.5 to 130 nm. Proc. R. Soc. Lond. A Math. Phys. Sci. 1972;331:19–38. doi: 10.1098/rspa.1972.0162. - DOI
-
- Palasantzas G., van Zwol P.J., De Hosson J.T.M. Transition from Casimir to van der Waals force between macroscopic bodies. Appl. Phys. Lett. 2008;93:121912. doi: 10.1063/1.2992030. - DOI
-
- Boström M., Sernelius B.E., Brevik I., Ninham B.W. Retardation turns the van der Waals attraction into a Casimir repulsion as close as 3 nm. Phys. Rev. A. 2012;85:010701. doi: 10.1103/PhysRevA.85.010701. - DOI
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources

