Deformation Estimation of Textureless Objects from a Single Image
- PMID: 39066104
- PMCID: PMC11280557
- DOI: 10.3390/s24144707
Deformation Estimation of Textureless Objects from a Single Image
Abstract
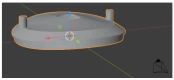
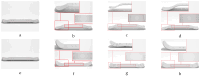
Deformations introduced during the production of plastic components degrade the accuracy of their 3D geometric information, a critical aspect of object inspection processes. This phenomenon is prevalent among primary plastic products from manufacturers. This work proposes a solution for the deformation estimation of textureless plastic objects using only a single RGB image. This solution encompasses a unique image dataset of five deformed parts, a novel method for generating mesh labels, sequential deformation, and a training model based on graph convolution. The proposed sequential deformation method outperforms the prevalent chamfer distance algorithm in generating precise mesh labels. The training model projects object vertices into features extracted from the input image, and then, predicts vertex location offsets based on the projected features. The predicted meshes using these offsets achieve a sub-millimeter accuracy on synthetic images and approximately 2.0 mm on real images.
Keywords: deformation estimation; graph convolution; image dataset; label generation; single image; textureless deformed object.
Conflict of interest statement
Authors Joshua K. Pickard and Ganyun Sun were employed by the company Eigen Innovations. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Figures







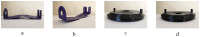






















References
-
- Lowe D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004;60:91–110. doi: 10.1023/B:VISI.0000029664.99615.94. - DOI
-
- Bay H., Tuytelaars T., Van Gool L. SURF: Speeded Up Robust Features. In: Leonardis A., Bischof H., Pinz A., editors. Computer Vision—ECCV 2006. Volume 3951. Springer; Berlin/Heidelberg, Germany: 2006. pp. 404–417. Lecture Notes in Computer Science. - DOI
-
- Moemen M.Y., Elghamrawy H., Givigi S.N., Noureldin A. 3-D reconstruction and measurement system based on multimobile robot machine vision. IEEE Trans. Instrum. Meas. 2021;70:5003109. doi: 10.1109/TIM.2020.3026719. - DOI
-
- Wang Y., James S., Stathopoulou E.K., Beltrán-González C., Konishi Y., Del Bue A. Autonomous 3-D reconstruction, mapping, and exploration of indoor environments with a robotic arm. IEEE Trans. Robot. Autom. Lett. 2019;4:3340–3347. doi: 10.1109/LRA.2019.2926676. - DOI
Grants and funding
LinkOut - more resources
Full Text Sources

