Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2025 Jul;32(5):654-674.
doi: 10.1177/10731911241260545. Epub 2024 Jul 27.

Continuous Norming Approaches: A Systematic Review and Real Data Example

Julian Urban  1   2 , Vsevolod Scherrer  1 , Anja Strobel  3 , Franzis Preckel  1
Affiliations

Continuous Norming Approaches: A Systematic Review and Real Data Example

Julian Urban et al. Assessment. 2025 Jul.

Abstract

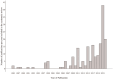
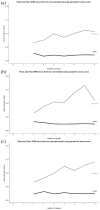
Norming of psychological tests is decisive for test score interpretation. However, conventional norming based on subgroups results either in biases or require very large samples to gather precise norms. Continuous norming methods, namely inferential, semi-parametric, and (simplified) parametric norming, propose to solve those issues. This article provides a systematic review of continuous norming. The review includes 121 publications with overall 189 studies. The main findings indicate that most studies used simplified parametric norming, not all studies considered essential distributional assumptions, and the evidence comparing different norming methods is inconclusive. In a real data example, using the standardization sample of the Need for Cognition-KIDS scale, we compared the precision of conventional, semi-parametric, and parametric norms. A hierarchy in terms of precision emerged with conventional norms being least precise, followed by semi-parametric norms, and parametric norms being most precise. We discuss these findings by comparing our findings and methods to previous studies.

Keywords: GAMLSS; cNORM; continuous norming; need for cognition; norm generation; regression-based norming; systematic review.

PubMed Disclaimer

Conflict of interest statement

Declaration of Conflicting InterestsThe author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Figures

Figure 1.
Figure 1.
Association of Norm Predictor and Fictional Raw Scores. Note. Dashed lines indicate boundaries of subgroups. Red lines show the median for these subgroups. The orange arrow refers to within-subgroup bias, the gray arrow to transition bias. The blue error displays the rationale of our within-subgroup bias proxy. The gray curve displays a continuous relationship of raw scores and norm predictor age.
Figure 2.
Figure 2.
Study Identification and Screening Process as a PRISMA Chart. Note. This figure presents the literature search and gives information on the number of coded studies. k = number of publications, h = number of included studies.
Figure 3.
Figure 3.
Number of Publications per Year. Note. Number of cases N = 189.
Figure 4.
Figure 4.
Percentile Plot (a), First-Order Derivative of Norming Regression Function (b), and Deviation Plot Between Observed and Fitted Norm Scores for the Different Age Groups (c) for Semi-Parametric Norming Model. Note. Model-implied percentiles (lines) align with observed percentiles (dots) in the percentile plot and shows no intersections (a). The first-order derivative of the norming regression function does not indicate zero-crossings (b). The deviation plot shows pp-plots for the modeled age subgroups, where only small deviations between model-implied and observed percentiles occur (c). Combined, this implies a good absolute fit.
Figure 5.
Figure 5.
Worm Plot (a) and Percentile Plot (b) of BB-Model of Parametric Norming. Note. The blue bars above the worm plots (a) indicate the age range for each of the four plots arranged in rows. The youngest age quantile is represented in the bottom left plot (1), while the eldest is shown in the top right plot (4). The worm plots are flat and generally fall between the two semi-circles, indicating a good absolute fit. In the percentile plot (b), dots represent observed percentiles dependent on age, and each line corresponds to a raw score indicating the model-implied percentile with respect to age. The plot demonstrates a monotonically increasing trend, suggesting a low likelihood of overfitting.
Figure 6.
Figure 6.
Maximum Values of Transition Bias (a) and Within-Subgroup Bias (b) for Parametric, Semi-Parametric, and Conventional Norms. Note. We computed bias for just eight subgroups for conventional norms by setting the minimum subgroup sample size to n = 20.
Figure 7.
Figure 7.
Mean and Maximum Absolute Differences Between Individual Norm-Scores.
See this image and copyright information in PMC

References

    1. Akaike H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6), 716–723. 10.1109/TAC.1974.1100705 - DOI
    1. Akaike H. (1983). Statistical inference and measurement of entropy. In Box G. E. P., Leonard T., Wu C.-F. (Eds.), Scientific inference, data analysis, and robustness (pp. 165–189). Elsevier. 10.1016/B978-0-12-121160-8.50015-6 - DOI
    1. American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for educational and psychological testing. American Educational Research Association.
    1. Bates D., Mächler M., Bolker B., Walker S. (2015). Fitting linear mixed-effects models using lme4. Journal of Statistical Software, 67(1), 1–48. 10.18637/jss.v067.i01 - DOI
    1. Brandt H., Moosbrugger H. (2020). Planungsaspekte und Konstruktionsphasen von Tests und Fragebogen. In Moosbrugger H., Kelava A. (Eds.), Testtheorie und Fragebogenkonstruktion (pp. 39–66). Springer.

Publication types

LinkOut - more resources