Super Resolution of Magnetic Resonance Images

Abstract

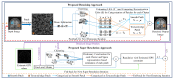
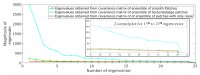
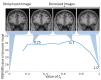
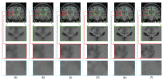
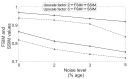
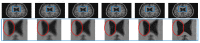
In this work, novel denoising and super resolution (SR) approaches for magnetic resonance (MR) images are addressed, and are integrated in a unified framework, which do not require example low resolution (LR)/high resolution (HR)/cross-modality/noise-free images and prior information of noise-noise variance. The proposed method categorizes the patches as either smooth or textured and then denoises them by deploying different denoising strategies for efficient denoising. The denoising algorithm is integrated into the SR approach, which uses a gradient profile-based constraint in a sparse representation-based framework to improve the resolution of MR images with reduced smearing of image details. This constraint regularizes the estimation of HR images such that the estimated HR image has gradient profiles similar to the gradient profiles of the original HR image. For this, the gradient profile sharpness (GPS) values of an unknown HR image are estimated using an approximated piece-wise linear relation among GPS values of LR and upsampled LR images. The experiments are performed on three different publicly available datasets. The proposed SR approach outperforms the existing unsupervised SR approach addressed for real MR images that exploits low rank and total variation (LRTV) regularization, by an average peak signal to noise ratio (PSNR) of 0.73 dB and 0.38 dB for upsampling factors 2 and 3, respectively. For the super resolution of noisy real MR images (degraded with 2% noise), the proposed approach outperforms the LRTV approach by an average PSNR of 0.54 dB and 0.46 dB for upsampling factors 2 and 3, respectively. The qualitative analysis is shown for real MR images from healthy subjects and subjects with Alzheimer's disease and structural deformity, i.e., cavernoma.

Keywords: MRI; enhancement; reconstruction; self-similarity; super resolution.

Figure 1

Detailed illustration of the proposed approach.

Figure 2

Demonstration of eigenvalues obtained from an ensemble of smooth patches (green) and textured/edge patches (cyan) present in a randomly selected magnetic resonance (MR) image degraded with 2% Rician distributed noise. The eigenvalues for patches with only noise are shown in red color. The x-axis denotes the number of eigenvector and the y-axis denotes the corresponding eigenvalue. The plot is zoomed for the 15th to the 25th eigenvectors and is shown to better visualize the small differences among eigenvalues. Here, 2% noise denotes that noise variance is $0.02\times 255=5.1$ for an image with 255 as its maximum pixel intensity.

Figure 3

(a) Illustration of the relation between distribution of LRA-based reconstruction error values ($\mathbf{e}$) of an ensemble of image patches and strength of noise, i.e., noise variance. (b) Illustration of the relation between mean of reconstruction error values with strength of noise, i.e., noise variance.

Figure 4

Demonstration of the relation between reconstruction error vector $\mathbf{e}$ and patch structure, i.e., smooth and textured/edge, using the noise adaptive threshold ${\tau }_1$, for (mean subtracted patches of) a randomly selected image corrupted with 2% Rician distributed noise: (a) Histogram of reconstruction error values $\mathbf{e}$ and the corresponding image, (b) histogram of reconstruction error values less than ${\tau }_1$ and the corresponding patches in the image, and (c) histogram of reconstruction error values greater or equal to ${\tau }_1$ and the corresponding patches in the image.

Figure 5

Illustration of major steps in the proposed denoising approach.

Figure 6

Demonstration of image denoising achieved by different denoising algorithms on real MR images with synthetically added 2% Gaussian noise. From left to right—noisy image, optimized blockwise non local means (ONLM) [57], multi-resolution based ONLM (MRONLM) [41], oracle based discrete cosine transform (ODCT), PCA-based denoising over ODCT (PRINLM) [35], variance stabilized transform with blockwise matching and 4D filtering (VST-BM4D) [25], adaptive ONLM (AONLM) [40], the proposed approach, and the original noiseless image.

Figure 7

Illustration of the significance of the proposed categorization of smooth and textured/edge patches and progressive estimation of eigenvectors by adapting it with the existing low-rank approximation (LRA)-based denoised approach [15]. (a) Noisy image (3% Rician Noise), (b) denoised using the existing LRA-based denoising approach [15], (c) the proposed denoising approach, (d) the existing approach [15] adapted with the proposed patch categorization and re-estimation of eigenvectors, (e) noise-free image.

Figure 8

Analysis of parameter ${\zeta }_1$ for optimal selection of ${\tau }_1={\zeta }_1{\sum }_{i=1}^N{e}_i$, $e_i$ denotes the low rank-based reconstruction error of the ith patch and N denotes the number of patches, for categorization of the patch as smooth or textured/edge in the proposed denoising approach. The peak signal to noise ratio (PSNR) values are computed for an MR image denoised using different values of ${\zeta }_1$, and plotted in this Figure. The denoised images using ${\zeta }_1$ as 0.25, 0.7 and 1.0 are also shown to indicate the reason for rise and drop in PSNR values.

Figure 9

Illustration of reconstruction results for real MR image volume for super-resolution factor 2 using different super-resolution algorithms: (a) nearest neighbor interpolation, (b) spline interpolation, (c) non-local means [13], (d) low rank and total variation (LRTV) [12], (e) the proposed method, and (f) the original denoised high resolution (HR) image. Zoomed version of the red box shown in the axial slice is shown to demonstrate the difference (specifically in tissue boundaries indicated with arrows).

Figure 10

Demonstration of PSNR, structural similarity index (SSIM) and feature similarity index metric (FSIM) values obtained for super resolution of eight MR image volumes by upscale factors 2 and 3.

Figure 11

Illustration of super resolution results for structural deformity cavernoma in real MR images, by different algorithms: (a) nearest neighbor, (b) spline interpolation, (c) non local means in three dimensions (NLM3D) [13], (d) low rank total variation based method (LRTV) [12], (e) the proposed approach, and (f) the original HR image. Each slice in axial, sagittal, and coronal planes is shown. The zoomed version of the cavernoma region from the coronal slice is highlighted in red rectangle. Please zoom for better visualization.

Figure 12

Optimal selection of parameter $\lambda$ in the super resolution approach. A random MR image is selected and upscaled by factor 2 using the proposed super-resolution (SR) approach. The HR image is obtained with different values of $\lambda$ in Equation (3), and the obtained PSNR values are plotted.

Figure 13

Demonstration of reconstruction quality of different kinds of regions/patches, region with edges (green boxes), region with texture (red boxes), and smooth region (cyan boxes), after super resolving real MR images degraded with downsampling factor 2 and 2% noise, using different algorithms. (a) NN interpolation of noisy LR image, (b) spline interpolation of denoised LR image, (c) NLM3D [13] applied on denoised LR image, (d) LRTV [12] applied on denoised LR images, (e) the proposed work applied on a noisy LR image, and (f) the original noise-free HR image.

Figure 14

Analysis of FSIM and SSIM values for different noise variances and upscale factors.

Figure 15

Illustration of super resolving the real MR images of an Alzheimer’s subject degraded with downsampling factor 2 and 2% noise. From Left: Interpolated noisy LR image, spline interpolation of denoised image, NLM3D-based super-resolved denoised image, LRTV-based super resolution of the denoised image, the proposed approach super resolving the noisy LR image, and the original noiseless HR image.