Probabilistic neural transfer function estimation with Bayesian system identification

Abstract

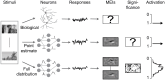
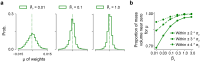
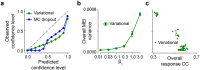
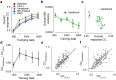
Neural population responses in sensory systems are driven by external physical stimuli. This stimulus-response relationship is typically characterized by receptive fields, which have been estimated by neural system identification approaches. Such models usually require a large amount of training data, yet, the recording time for animal experiments is limited, giving rise to epistemic uncertainty for the learned neural transfer functions. While deep neural network models have demonstrated excellent power on neural prediction, they usually do not provide the uncertainty of the resulting neural representations and derived statistics, such as most exciting inputs (MEIs), from in silico experiments. Here, we present a Bayesian system identification approach to predict neural responses to visual stimuli, and explore whether explicitly modeling network weight variability can be beneficial for identifying neural response properties. To this end, we use variational inference to estimate the posterior distribution of each model weight given the training data. Tests with different neural datasets demonstrate that this method can achieve higher or comparable performance on neural prediction, with a much higher data efficiency compared to Monte Carlo dropout methods and traditional models using point estimates of the model parameters. At the same time, our variational method provides us with an effectively infinite ensemble, avoiding the idiosyncrasy of any single model, to generate MEIs. This allows us to estimate the uncertainty of stimulus-response function, which we have found to be negatively correlated with the predictive performance at model level and may serve to evaluate models. Furthermore, our approach enables us to identify response properties with credible intervals and to determine whether the inferred features are meaningful by performing statistical tests on MEIs. Finally, in silico experiments show that our model generates stimuli driving neuronal activity significantly better than traditional models in the limited-data regime.

Fig 1. Schematic of neural system identification for predicting responses.

Biological neurons (top row; second column) respond to visual stimuli (first column) distinctly (third column), with an unknown MEI (fourth column) driving a cell with optimal activation (sixth column). Traditional system identification methods (center row) learn stimulus-response function and yield a MEI with unknown statistics (fifth column). Bayesian approaches (bottom row) learn distributions of model parameters to predict neuronal responses, yielding infinite MEIs, whose significance map can be computed by sampling from posterior, to drive a neuron with credible intervals.

Fig 2. Hyperparameter β_v for regulating weight sparseness.

(a) Distribution of the means (μ) of model weights for different β_v values. Dotted lines indicate distribution means. (b) Ratio of mass volume near zero for the distributions in (a). Note that with our setup, if we use a mixture of two Gaussians for the posterior, we would not observe a higher weight sparseness with a larger β_v; rather, we would observe a wider distribution of model parameters.

Fig 3. Neural prediction with weight uncertainty.

(a) Mean recorded responses (gray) and predictive responses to natural stimuli(black, baseline; red, L2+L1; green, variational one with β_v = 0.1; blue, MC dropout with dropout rate 70%; shaded green and blue representing standard deviation for the variational and the dropout methods, respectively), estimated MEIs, as well as standard deviation of MEI (MEI_std; only for two probabilistic models), for two exemplary neurons. MEI and MEI_std use different color scales with red and blue indicating positive and negative values, respectively. Note that MEI has much larger absolute values than MEI_std. (b) Predictive performance (RMSE) based on test data with different amounts of training data (left, 50% of training data, p = 0.004 for variational vs. baseline, p = 0.0024 for variational vs. ensemble, p = 0.0006 for variational vs. L2+L1, p = 0.0186 for variational vs. MC dropout, p = 0.549 for variational vs. MAP, two-sided permutation test with n = 10,000 repeats; right, 100% of data, p = 0.0001 for variational vs. baseline, p < 0.0001 for variational vs. ensemble, p = 0.0001 for variational vs. L2+L1, p < 0.0001 for variational vs. MC dropout, p = 0.0001 for variational vs. MAP) for 6 models (red dash, ensemble; cyan, MAP; 10 seeds per model). (c) Same with (b), but using log likelihood to evaluate models (left, p < 0.0001 for variational vs. baseline, p < 0.0001 for variational vs. ensemble, p < 0.0001 for variational vs. L2+L1, p < 0.0001 for variational vs. MC dropout, p = 0.0001 for variational vs. MAP; right, p = 0.0001 for variational vs. baseline, p = 0.0001 for variational vs. ensemble, p = 0.0001 for variational vs. L2+L1, p = 0.0001 for variational vs. MC dropout, p = 0.0001 for variational vs. MAP). (d) Same with (b), but using CC to evaluate models (left, p = 0.028 for variational vs. baseline, p = 0.0043 for variational vs. ensemble, p = 0.0009 for variational vs. L2+L1, p = 0.082 for variational vs. MC dropout, p = 0.2526 for variational vs. MAP; right, p = 0.0001 for variational vs. baseline, p = 0.013 for variational vs. ensemble, p = 0.0007 for variational vs. L2+L1, p = 0.6159 for variational vs. MC dropout, p = 0.0001 for variational vs. MAP), with another model used by [13] (red triangle). (e) Predictive model performance (CC) for different β_v values. Error bars in (b)—(e) represent standard deviation of n = 10 random seeds for each model.

Fig 4. Neural transfer functions with variability.

(a) Calibration analysis for the variational model and the MC dropout model. The dashed line indicates a perfect calibration curve. (b) Overall MEI variance for different β_v values (10 seeds per model). (c) Scatter plot of overall response CC and overall MEI variance for 6 β_v values and 10 seeds (each dot representing one model at each β_v and each seed). Error bars in (b) represent standard deviation of n = 10 random seeds for each model.

Fig 5. Variational models on the second dataset.

(a) Model performance based on test data of the second dataset with different amounts of training data for five models (n = 10 random seeds per model). p = 0.0238 for variational vs. L2+L1 at 20% of training data, p < 0.0001 at 40%, p = 0.0001 at 60%, p = 0.0042 at 80%, p = 0.1096 at 100%. (b) Overall MEI variance for different amounts of training data for variational models (10 seeds per model). (c) Scatter plot for overall response CC and overall MEI variance for different amounts of training data and at 10 seeds. Each dot representing one model. (d) Performance difference between the variational and the L2+L1 models. (e) Scatter plot of model predictions for the variational model and the L2+L1 model at one random seed when using 40% training data. Each dot representing one neuron. (f) Like (e) but using 100% training data. Error bars in (a), (b) and (d) represent standard deviation of n = 10 random seeds for each model.

Fig 6. In silico experiments of neuronal activity with derived MEIs.

(a) Activation distributions of 6 exemplary neurons driven by the 6 verified MEIs (green and gray representing the respective MEI and remaining MEIs, respectively). (b) Response matrix of each neuron activated by the verified MEIs of all neurons. Scaling was applied to each row to ensure that the maximum of the responses to all stimuli is equal to one. (c) Estimated MEIs for L2+L1 (first row) and variational (second row) models, MEI_std (third row), as well as significance map (fourth row; white, p < 0.01, one-sample two-sided permutation test against zero for 10,000 repeats), for three exemplary neurons when using 40% of training data. MEI and MEI_std in the UV channel, with different color scales. Note that MEI has much larger absolute values than MEI_std. (d) 1D histogram of neuronal activity driven by the generated MEIs from the variational model for Neuron 1 when using 40% of training data. Insets: example MEIs with corresponding activation indicated by dotted lines (red, maximum of L2+L1; green, variational). (e) Scatter plot of activation driven by MEIs yielded from variational (using the weight mean μ) and L2+L1 models at one random seed when using 40% of training data. Each dot representing one cell. (f,g,h) Same with (c), (d) and (e), but using 100% of training data.