Quantum thermodynamics with a single superconducting vortex

Abstract

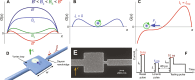
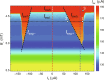
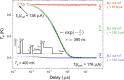
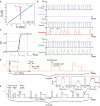
We demonstrate complete control over dynamics of a single superconducting vortex in a nanostructure, which we coin the Single Vortex Box. Our device allows us to trap the vortex in a field-cooled aluminum nanosquare and expel it on demand with a nanosecond pulse of electrical current. Using the time-resolving nanothermometry we measure [Formula: see text] joules as the amount of the dissipated heat in the elementary process of the single-vortex expulsion. Our experiment enlightens the thermodynamics of the absorption process in the superconducting nanowire single-photon detectors, in which vortices are perceived to be essential for a formation of a detectable hotspot. The demonstrated opportunity to manipulate a single superconducting vortex reliably in a confined geometry comprises a proof of concept of a nanoscale nonvolatile memory cell with subnanosecond write and read operations, which offers compatibility with quantum processors based either on superconducting qubits or on rapid single-flux quantum circuits.

Fig. 1.. Single Vortex Box (SVB).

(A) Landscape of the Gibbs free energy of a single-vortex state across the width of the box at various magnetic fields B_⊥ and with no applied current I_L. For B_⊥ > B₀, the state with vortex becomes energetically favorable when sample is cooled across T_c. (B and C) The effect of the applied current on the tilt of the potential energy. For I_L = I_exp, the dependence shows no minimum that would stabilize the vortex, and it leaves the sample pushed out by the Lorentz force F_L. I_exp grows with the field because vortex is stronger bound in local energy minimum further away from the transition field B₀. (D) Layout of the studied nanostructure consisting of an SVB, a Dayem nanobridge, and connecting leads. The Lorentz force exerted on the vortex by the applied current I_L in the presence of perpendicular magnetic field B_⊥ is depicted schematically. (E) Scanning electron microscopy image of the working aluminum device. (F) The pulse protocol used in the experiment.

Fig. 2.. Electrical probing and manipulation of the vortex state.

(A) Switching current of the nanobridge versus perpendicular magnetic field I_sw(B_⊥) reveals a pronounced dip in the characteristics for the field values where the entry of a single vortex is expected. Here, only the reset and testing pulses are used (cf. Fig. 1F). (B) I_sw(B_⊥) dependence in the region of the dip. The red curve is a detailed measurement of the region of the suppressed switching current I_swl visible in the curve of (A) inside the dashed frame, and the blue curve presents the effect of the application of the additional pulse, called the Lorentz pulse (cf. Fig. 1F). It is high enough to expel the vortex but too low to switch the bridge. The following testing pulse probes the box in the Meissner state: This time, there is no vortex to be expelled. Consequently, there are no QPs excited in the box, and the switching current remains at its high value I_swh. (C) Switching current of the nanobridge as a function of the Lorentz pulse amplitude recorded at the fixed magnetic field in the dip region [dashed vertical line in (B)]. For low values of the Lorentz pulse (region 1), it can neither expel vortex nor switch the bridge. In region 2, Lorentz pulse can expel the vortex but not switch the bridge. Last, for the highest values of the Lorentz pulse (region 3), it first expels the vortex and then switches the bridge. The bath temperature is T₀ = 400 mK.

Fig. 3.. The as-received experimental vortex stability diagram I_sw(B_⊥, I_L).

Switching current dependence of the nanobridge on the applied perpendicular magnetic field B_⊥ and the amplitude of the Lorentz pulse I_L. It reveals range of magnetic fields in which vortex can be expelled with sufficiently high Lorentz pulse without switching the bridge. This range is marked by the existence of the two triangles in the diagram. The inner slopes of triangles (indicated with dashed lines) mark the minimum value of the Lorentz pulse necessary to expel the vortex I_exp(B_⊥). The outer edges correspond to the switching thresholds of the device, i.e., when I_L exceeds these thresholds, it necessarily switches the bridge and, thus, effectively works as the second reset pulse. The switching current (measured with the testing pulse) is low when it has to expel the vortex from the box and high if the box is in the Meissner state. The two cross sections of the diagram that are denoted with the vertical dashed lines are presented in Fig. 2B. The horizontal dashed line marks the cross section visible in Fig. 2C. The indicated points 1 to 3 refer to Fig. 4. The extended discussion of the vortex stability diagram is provided in fig. S7.

Fig. 4.. Experimental thermal dynamics of the SVB after expulsion of a single vortex.

We apply the IL = 130.3 μA at B_⊥ = 4.6 mT to get rid of the vortex and observe the following thermal transient of the box (curve 1). The other two curves are references revealing no electron temperature variation after the application of either a too low Lorentz pulse to expel the vortex (I_L = 67.8 μA, curve 2) or a too low magnetic field to trap the vortex after the application of the reset pulse (B_⊥ = 4.4 mT, curve 3). In the case of the curve 2, the testing pulse itself expels the vortex. It results in the elevated value of the probed temperature, which is independent of the delay. The broken line, imposed on the curve 1, represents the exponential fit in the linear regime. The three points (I_L, B_⊥), corresponding to the three curves, are imposed on the vortex stability diagram in Fig. 3.

Fig. 5.. Measurement of the switching probability.

(A) The current-voltage characteristics of a similar device to the one studied in this work. The supercurrent branch reveals the switching current of the nanobridge. (B) The fragments of trains of testing pulses, for three different amplitudes and their voltage response recorded on the device. The voltage drop appears when the nanobridge is switched to the normal state. (C) The dependence of nanobridge switching probability on the testing pulse amplitude, usually called the S curve. The three imposed points (I_TEST for switching probability equal to 0, 0.6, and 1) correspond to the amplitudes of the pulses from (B). (D) The actual train of N testing pulses: Each pulse consists of a short probing part (testing the switching probability of the bridge), followed by a long sustain section (necessary to read out the switching events with low pass–filtered twisted pairs f_cut ≈ 80 kHz). (E) To manipulate the vortex, we add the two pulses to the each cycle of the standard probing protocol (D): reset pulse I₀ to overheat the SVB above T_c and allow the field cooling of the SVB and Lorentz pulse I_L to exert force F_L on the vortex. The real shapes of the pulses, as visualized on the scope, are provided in the insets. The finite rising and trailing edges of the pulses are limited by the finite bandwidth of the arbitrary waveform generator (BW = 120 MHz). For on-chip imaging of the pulses, see appendix A of (15).

Fig. 6.. The conversion of the switching current to temperature.

The transformation of the I_sw(delay) into a temporal evolution of the temperature T(delay) with the application of the calibration curve I_sw(T). An exemplary conversion for a single point is displayed with arrows. The I_sw(T) curve bears information about values of the junction switching current at different electron temperatures. It is measured at fixed bath temperatures with electrons thermalized to the lattice.