Signature of anyonic statistics in the integer quantum Hall regime

Abstract

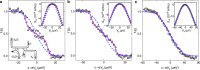
Anyons are exotic low-dimensional quasiparticles whose unconventional quantum statistics extend the binary particle division into fermions and bosons. The fractional quantum Hall regime provides a natural host, with the first convincing anyon signatures recently observed through interferometry and cross-correlations of colliding beams. However, the fractional regime is rife with experimental complications, such as an anomalous tunneling density of states, which impede the manipulation of anyons. Here we show experimentally that the canonical integer quantum Hall regime can provide a robust anyon platform. Exploiting the Coulomb interaction between two copropagating quantum Hall channels, an electron injected into one channel splits into two fractional charges behaving as abelian anyons. Their unconventional statistics is revealed by negative cross-correlations between dilute quasiparticle beams. Similarly to fractional quantum Hall observations, we show that the negative signal stems from a time-domain braiding process, here involving the incident fractional quasiparticles and spontaneously generated electron-hole pairs. Beyond the dilute limit, a theoretical understanding is achieved via the edge magnetoplasmon description of interacting integer quantum Hall channels. Our findings establish that, counter-intuitively, the integer quantum Hall regime provides a platform of choice for exploring and manipulating quasiparticles with fractional quantum statistics.

Fig. 1. Experimental setup.

a In the presence of two strongly coupled quantum Hall channels at ν = 2, tunneling electrons e (individual red wave-packets) progressively split into two pairs (circled). The fast ‘charge’ pair (blue background) consists of two copropagating e/2 wave-packets, one in each channel, whereas the slow ‘neutral’ pair (green background) consists of opposite  ± e/2 charges. The fractionalized e/2 charges propagate toward a central QPC (yellow split gates) of transmission τ_c, used to investigate their quantum statistics from the outgoing current cross-correlations. The strong coupling regime and the degree of fractionalization at the level of the central QPC are established separately through the evolution of the electron energy distribution function f(ε) from a non-equilibrium double step (red inset) to a smoother function (magenta inset). b Illustration of the time-braiding mechanism, whereby an impinging fractionalized e/2 charge (red) braids with an electron-hole pair (black) spontaneously excited at the central QPC. c E-beam micrograph of the sample. The two copropagating edge channels are drawn as black lines with arrows indicating the chirality. The aluminum gates used to form the QPCs by field effect are highlighted in false colors (sources in red, central analyzer in yellow). A negative voltage is applied to the non-colored gates to reflect the edge channels at all times. Tunneling at the sources is controlled by the applied dc voltages V_1,2,3,4 and through their gate-controlled transmission probability τ_s.

Fig. 2. Spectroscopy of the electron energy distribution f(ε).

The shape of f(ε) reflects the inter-channel coupling regime and informs on the conditions for a complete charge fractionalization at the central QPC. One source is voltage biased at V_s, here with τ_s ≈ 0.5, and the same probe voltage V_p is applied across the other one (see schematic in a). Circles and triangles show data points with the voltage biased source QPC on the left and right side, respectively. Purple continuous lines and blue dashed lines represent exact theoretical predictions in the strong coupling regime for a time delay between charge and neutral pairs of δt = 64 ps and ∞, respectively (see Supplementary Information). Insets: Cross-correlations S₁₂ versus probe voltage V_p. Main panels: f(ε) obtained by differentiation of S₁₂, see Eq. (1), with τ_c ≃ 0.5. a–c: Data and theory at T ≃ 11 mK for a source voltage V_s =  23 μV, 35 μV, and 70 μV, respectively.

Fig. 3. Cross-correlation signature of fractional statistics with symmetric dilute beams.

a Measured left/right source QPC dc transmission as a function of bias voltage, shown in light/dark blue, respectively. b Sum of sources' shot noise S_Σ vs source bias voltage V_s. The orange lines display Eq. (3) with T = 11 mK, the independently measured temperature. c Measured excess shot noise S₁₂/(τ_c(1 − τ_c)) as a function of source shot noise S_Σ for a small source QPC transmission τ_s = 0.05/0.95 (full/empty dots respectively). The purple lines display the strong inter-channel coupling prediction for δt = 64 ps. The green lines denotes the slope, i.e., the Fano factor (see Main text), yielding P ≃ −0.38/−0.56 for τ_s = 0.05/0.95 respectively. In all panels full/open circles and solid/dashed lines denote τ_s = 0.05/0.95, respectively.

Fig. 4. Cross-correlations vs dilution of symmetric beams.

Main panels and insets show, respectively, the generalized Fano factor P and the renormalized cross-correlations S₁₂(V_s = 70 μV)/(τ_c(1 − τ_c)) vs the outer edge channel transmission τ_s of the symmetric source QPCs. Symbols are data points. Blue lines are high bias/long δt predictions. Purple lines are S₁₂(V_s = 70 μV)/(τ_c(1 − τ_c)) predictions at δt = 64 ps. a The cross-correlation signal and corresponding P_outer (open circles) are measured by partially transmitting at the central QPC (τ_c ≈ 0.5) the same outer edge channel (black) where electrons are tunneling at the sources (see schematics). This is the standard ‘collider’ configuration. b The cross-correlation signal and corresponding P_inner are obtained by setting the central QPC to partially transmit (τ_c ≈ 0.5) the inner edge channel (grey), whereas electrons are tunneling into the outer edge channel at the sources (see schematic). In this particular configuration, the source shot noise does not directly contribute to the cross-correlation signal. Filled symbols in the main panel display P_outer − 1, with P_outer the data in a and  − 1 corresponding to the subtraction of the source shot noise.