A novel kinetic model to demonstrate the independent effects of ATP and ADP/Pi concentrations on sarcomere function

Abstract

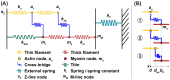
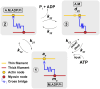
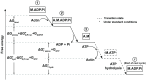
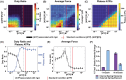
Understanding muscle contraction mechanisms is a standing challenge, and one of the approaches has been to create models of the sarcomere-the basic contractile unit of striated muscle. While these models have been successful in elucidating many aspects of muscle contraction, they fall short in explaining the energetics of functional phenomena, such as rigor, and in particular, their dependence on the concentrations of the biomolecules involved in the cross-bridge cycle. Our hypothesis posits that the stochastic time delay between ATP adsorption and ADP/Pi release in the cross-bridge cycle necessitates a modeling approach where the rates of these two reaction steps are controlled by two independent parts of the total free energy change of the hydrolysis reaction. To test this hypothesis, we built a two-filament, stochastic-mechanical half-sarcomere model that separates the energetic roles of ATP and ADP/Pi in the cross-bridge cycle's free energy landscape. Our results clearly demonstrate that there is a nontrivial dependence of the cross-bridge cycle's kinetics on the independent concentrations of ATP, ADP, and Pi. The simplicity of the proposed model allows for analytical solutions of the more basic systems, which provide novel insight into the dominant mechanisms driving some of the experimentally observed contractile phenomena.

Fig 1. Schematic of a half-sarcomere.

(A) Half-sarcomere model showing the geometry of a system containing two actin nodes and two myosin nodes. Cross-bridges are bound, connecting the thick and thin filaments. (B) Schematic showing the three potential mechanical states of a cross-bridge. State 1 shows a cross-bridge unbound from the thin filament. State 2 shows a bound, pre-power stroke cross-bridge in a low force bearing state. State 3 shows a bound, post-power stroke cross-bridge in a high force bearing state. In state 3, the cross-bridge has also undergone a conformational change where the cross-bridge rest length (b₀) has shortened by the length of a power stroke (d_ps). The model is one dimensional, but this figure illustrates the model in two dimensions for clarity. All forces in this model are assumed to be one-dimensional, parallel to the filaments.

Fig 2. Schematic of the three-state system.

Shorthand for the biochemical states of the actomyosin complex are displayed in black frames: A-actin, M-myosin, ATP-adenosine triphophate, ADP-adenosine diphosphate, Pi-inorganic phosphate. All elements in each black box are bound. Between state 3 and state 1, ATP binds the actomyosin complex and is hydrolyzed. Rates for the transitions between each state are labeled such that k_ij represents the transition rate from state i to j. Association of ATP to the actomyosin complex and the dissociation of ADP and Pi from the actomyosin complex are indicated at the appropriate transition.

Fig 3. Schematic of free energy landscape for one full cycle.

Shorthand of the biochemical states of the actomyosin complex are framed in black (key in Fig 2 caption). Transition states are denoted by dashed lines and dashed frames. ΔG_hyd = ΔG_{T assoc.} + ΔG_{T hydr.} + ΔG_{D,Pi rel.}. Free energy of association of ATP is ΔG_{T assoc.}. Free energy of ATP hydrolysis is ΔG_{T hydr.}. Free energy of of ADP and Pi release from actomyosin is ΔG_{D,Pi rel.}. G_ADP,Pi = k_BT ln([ADP][Pi]). G_ATP = k_BT ln([ATP]). Note: The free energies of each state depicted in this free energy landscape assume there is no cross-bridge deformation, and therefore do not include the elastic potential energy contributions of such deformations. The complete free energies of each state, including elastic potential energies, are fully defined in Eqs 2–5.

Fig 4. Model Implementation.

Single half-sarcomere consisting of 16 myosin and 24 actin nodes under (A-B) normal ([ATP] = 5 mM) and (C-D) reduced ([ATP] = 0.5μM) ATP conditions. (A,C) Force output profile denoted by black circles. Average force denoted by the dashed line. Force averaged over a sliding window of (A) 12 ms and (C) 14 ms denoted by blue lines with blue diamonds. (B,D) ATP consumption rate (molecules/s) denoted by black circles. ATP consumption rate averaged over a sliding window of 50 ms denoted by green diamonds.

Fig 5. One-myosin system simulations.

Comparison of free energy schema in terms of ATP consumption (A) Ratios of [ATP] to [ADP][Pi]. (B) Plateau ATP consumption rate for a one-myosin system where attachment of ATP and detachment of ADP and Pi effectively happen simultaneously, allowing for no time delay between these events. For such a model, the rate kinetics, and thus ATP consumption, depend only the ratio of [ATP]/[ADP][Pi]. (C) Our model’s plateau ATP consumption rate simulation results for a one-myosin system. Note the plot’s asymmetry compared to (B) and the proximity of the standard physiological conditions (bold red lines) to the crossover between regimes. One-myosin simulation results of (D) Duty ratio and (E) Average force for various ([ATP], [ADP][Pi]) combinations. (F) Changes in duty ratio (black), average force output (purple), and plateau ATP consumption rate (blue) at standard physiological [ADP][Pi] and varying [ATP] concentrations. (B-F) Standard physiological conditions are denoted by bold red lines ([ATP] = 5 mM, [ADP][Pi] = 0.09 mM²). Dashed white/gray lines denote the the [ATP] concentration associated with the onset of rigor ([ATP] = 0.5 mM) [75, 79]. (C-F) n = 10.

Fig 6. 16-myosin system simulations.

Results for 16-myosin simulations (n = 10) showing (A,D) Duty ratio, (B,E) Average force, and (C, D) Plateau ATP consumption rate. Average force and plateau ATP consumption rate are reported as per whole sarcomere. (D) Duty ratio and ATP consumption rate and (E) Average force at standard physiological [ADP][Pi] and varying [ATP] concentrations. (A-E) Standard physiological concentrations for [ATP] and [ADP][Pi] conditions are denoted by the bold red lines ([ATP] = 5 mM, [ADP][Pi] = 0.09 mM²). Dashed white/gray lines represent literature values of [ATP] concentrations where the onset of rigor has been observed experimentally ([ATP] = 0.5 mM) [75, 79]. (F) Percent of total elastic potential energy in the spring elements internal to the sarcomere (i.e. actin, myosin, titin, and cross-bridges) and external to the sarcomere (i.e. external spring).

Fig 7. Analytical results for a one-myosin system and varying parameters.

(A) Analytically calculated duty ratio (Eq 16) where the power stroke’s effective sliding distance (ESD) = 6 nm. (B) Analytically calculated average force (Eq 17) where ESD = 6 nm. (C) Analytically calculated ATP consumption rate (Eq 18) where ESD = 6 nm. (D) Analytically calculated duty ratio where ESD = d_ps = 7 nm, where 7 nm is the power stroke distance against no resistance. This causes an upward and rightward shift in the plot. (E) Analytically calculated duty ratio where ESD = 3 nm. This causes a downward and leftward shift in the plot. (F) Analytically calculated duty ratio where ESD = 6 nm and k_ATP,0 = 7 × 10⁻⁵ s⁻¹. This causes a rightward shift in the plot. (A-I) Standard physiological concentrations for [ATP] and [ADP][Pi] conditions are denoted by the bold red lines ([ATP] = 5 mM, [ADP][Pi] = 0.09 mM²). Dashed white/gray lines denote the [ATP] concentration associated with the onset of rigor ([ATP] = 0.5 mM) [75, 79]. Effect of reducing k_ATP,0 on one-myosin analytical and 16-myosin simulation (n = 10) values for (G) Duty ratio, (H) Average force, and (I) Plateau ATP consumption rate at standard physiological [ADP][Pi] or increased [ADP][Pi] and varying [ATP] concentrations. Reducing k_ATP,0 causes a rightward shift in all of the plots. Increasing environmental [ADP][Pi] by a factor of 10³ alters 16 myosin system behavior. Average force and plateau ATP consumption rate are reported as per whole sarcomere. (H, inset) The one-myosin analytical system’s predictions of average force compared to muscle strip data (red circles) adapted from White [79]. Data are normalized to force under complete rigor, at [ATP] = 0.1 μM for the analytical system and [ATP] = 0mM for experimental data.