Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Jul 23:18:1403804.
doi: 10.3389/fnins.2024.1403804. eCollection 2024.

Bounding tractogram redundancy

Sanna Persson  1 , Rodrigo Moreno  1   2
Affiliations

Bounding tractogram redundancy

Sanna Persson et al. Front Neurosci. .

Abstract

Introduction: In tractography, redundancy poses a significant challenge, often resulting in tractograms that include anatomically implausible streamlines or those that fail to represent the brain's white matter architecture accurately. Current filtering methods aim to refine tractograms by addressing these issues, but they lack a unified measure of redundancy and can be computationally demanding.

Methods: We propose a novel framework to quantify tractogram redundancy based on filtering tractogram subsets without endorsing a specific filtering algorithm. Our approach defines redundancy based on the anatomical plausibility and diffusion signal representation of streamlines, establishing both lower and upper bounds for the number of false-positive streamlines and the tractogram redundancy.

Results: We applied this framework to tractograms from the Human Connectome Project, using geometrical plausibility and statistical methods informed by the streamlined attributes and ensemble consensus. Our results establish bounds for the tractogram redundancy and the false-discovery rate of the tractograms.

Conclusion: This study advances the understanding of tractogram redundancy and supports the refinement of tractography methods. Future research will focus on further validating the proposed framework and exploring tractogram compression possibilities.

Keywords: Bayesian estimation; Hoeffding's inequality; diffusion MRI; tractogram filtering; tractogram redundancy; tractography.

PubMed Disclaimer

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Figures

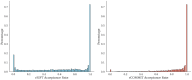
Figure 1
Figure 1
Distribution of rSIFT acceptance rates (Left) for accepted streamlines by rCOMMIT (acceptance rate = 1) and distribution of rCOMMIT rates for accepted streamlines by rSIFT (Right). The percentages are given for the total number of streamlines from all subjects in the dataset.
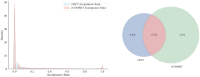
Figure 2
Figure 2
Distribution of the acceptance rate (Left) for rSIFT and rCOMMIT acceptance rates and the proportion of overlapping streamlines with a threshold of 1 (Right).
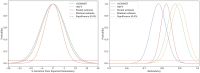
Figure 3
Figure 3
FDR estimation for subject ID 877168 in the HCP dataset using Hoeffding's inequality using different estimators of FDR. (Left) Deviation of the sampled FDR from its expected value. (Right) Hoeffding's upper-bound estimation of the FDR.
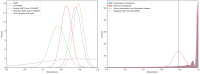
Figure 4
Figure 4
FDR upper-bound estimation using a Bayesian approach for subject ID 877168 in the HCP dataset. (Left) The estimate is determined by the width and the center of the distribution. (Right) In this example, the posterior and FDR histogram approximately coincide due to the extensive subsets for rSIFT and rCOMMIT, but generally, the posterior will be shifted in the direction of the prior for the model.
Figure 5
Figure 5
FDR upper bounds per subset size for different estimates of the streamline probabilities. (Left) Hoeffding's upper bound for log-normalized subset sizes for rSIFT and rCOMMIT. (Right) Bayesian upper bound for log-normalized subset sizes for rSIFT and rCOMMIT.
Figure 6
Figure 6
Visualization of the tractogram of Subject 877168 in HCP 10M. (Left) Tractogram filtering by rCOMMIT. (Middle) Tractogram filtering by rSIFT. (Right) Foundational streamlines at the intersection of filtering by rCOMMIT and rSIFT with acceptance probability = 1.
See this image and copyright information in PMC

References

    1. Astolfi P., Verhagen R., Petit L., Olivetti E., Sarubbo S., Masci J., et al. (2023). Supervised tractogram filtering using Geometric Deep Learning. Med. Image Anal. 90:102893. 10.1016/j.media.2023.102893 - DOI - PubMed
    1. Barakovic M., Tax C. M., Rudrapatna U., Chamberland M., Rafael-Patino J., Granziera C., et al. (2021). Resolving bundle-specific intra-axonal T2 values within a voxel using diffusion-relaxation tract-based estimation. Neuroimage 227:117617. 10.1016/j.neuroimage.2020.117617 - DOI - PMC - PubMed
    1. Basser P. J., Pajevic S., Pierpaoli C., Duda J., Aldroubi A. (2000). In vivo fiber tractography using DT-MRI data. Magn. Reson. Med. 44, 625–632. 10.1002/1522-2594(200010)44:4<625::AID-MRM17>3.0.CO;2-O - DOI - PubMed
    1. Bertò G., Bullock D., Astolfi P., Hayashi S., Zigiotto L., Annicchiarico L., et al. (2021). Classifyber, a robust streamline-based linear classifier for white matter bundle segmentation. Neuroimage 224:117402. 10.1016/j.neuroimage.2020.117402 - DOI - PubMed
    1. Chandio B. Q., Risacher S. L., Pestilli F., Bullock D., Yeh F.-C., Koudoro S., et al. (2020). Bundle analytics, a computational framework for investigating the shapes and profiles of brain pathways across populations. Sci. Rep. 10:17149. 10.1038/s41598-020-74054-4 - DOI - PMC - PubMed

LinkOut - more resources