Solid Boundary Output Feedback Control of the Stefan Problem: The Enthalpy Approach
- PMID: 39108930
- PMCID: PMC11301126
- DOI: 10.1109/tac.2022.3197704
Solid Boundary Output Feedback Control of the Stefan Problem: The Enthalpy Approach
Abstract
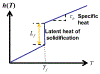
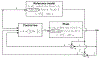
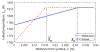
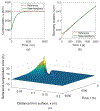
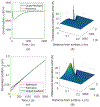
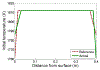
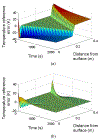
By taking enthalpy-an internal energy of a diffusion-type system-as the system state and expressing it in terms of the temperature profile and the phase-change interface position, the output feedback boundary control laws for a fundamentally nonlinear single-phase one-dimensional (1-D) PDE process model with moving boundaries, referred to as the Stefan problem, are developed. The control objective is tracking of the spatiotemporal temperature and temporal interface (solidification front) trajectory generated by the reference model. The external boundaries through which temperature sensing and heat flux actuation are performed are assumed to be solid. First, a full-state single-sided tracking feedback controller is presented. Then, an observer is proposed and proven to provide a stable full-state reconstruction. Finally, by combining a full-state controller with an observer, the output feedback trajectory tracking control laws are presented and the closed-loop convergence of the temperature and the interface errors proven for the single-sided and the two-sided Stefan problems. Simulation shows the exponential-like trajectory convergence attained by the implementable smooth bounded control signals.
Keywords: Control; Stefan problem; enthalpy; nonlinear partial differential equations; solidification.
Figures


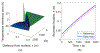
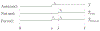


References
-
- Goodrich J, “Modern civilization relies on this crystal-growing method: The Czochralski method, an IEEE milestone, is used to grow single-crystal semiconductors for integrated circuits and photovoltaics,” IEEE Spectr. News, Inst, Dec. 6, 2019. [Online]. Available: https://spectrum.ieee.org/modern-civilization-relies-on-this-crystalgrow...
-
- Petrus B, Chen Z, Bentsman J, and Thomas BG, “Investigating dynamic thermal behavior of continuous casting of steel with CONOFFLINE,” Metallurgical Mater. Trans. B, vol. 51, no. 6, pp. 2917–2934, 2020.
-
- Rubinsteĭn LI, The Stefan Problem, no. v.27. Providence, RI, USA: Amer. Math. Soc., 1971.
-
- Das S, Klotz M, and Klocke F, “EDM simulation: Finite element-based calculation of deformation, microstructure and residual stresses,” J. Mater. Process. Technol, vol. 142, no. 2, pp. 434–451, Nov. 2003.
-
- King WE et al., “Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges,” Appl. Phys. Rev, vol. 2, no. 4, 2015, Art. no. 041304
Grants and funding
LinkOut - more resources
Full Text Sources
