Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2024 Aug 7;19(8):e0301301.
doi: 10.1371/journal.pone.0301301. eCollection 2024.

The performance of interrupted time series designs with a limited number of time points: Learning losses due to school closures during the COVID-19 pandemic

Florian D van Leeuwen  1 , Peter Lugtig  1 , Remco Feskens  2
Affiliations

The performance of interrupted time series designs with a limited number of time points: Learning losses due to school closures during the COVID-19 pandemic

Florian D van Leeuwen et al. PLoS One. .

Abstract

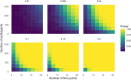
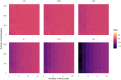
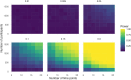
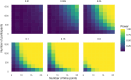
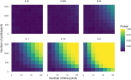
Interrupted time series (ITS) designs are increasingly used for estimating the effect of shocks in natural experiments. Currently, ITS designs are often used in scenarios with many time points and simple data structures. This research investigates the performance of ITS designs when the number of time points is limited and with complex data structures. Using a Monte Carlo simulation study, we empirically derive the performance-in terms of power, bias and precision- of the ITS design. Scenarios are considered with multiple interventions, a low number of time points and different effect sizes based on a motivating example of the learning loss due to COVID school closures. The results of the simulation study show the power of the step change depends mostly on the sample size, while the power of the slope change depends on the number of time points. In the basic scenario, with both a step and a slope change and an effect size of 30% of the pre-intervention slope, the required sample size for detecting a step change is 1,100 with a minimum of twelve time points. For detecting a slope change the required sample size decreases to 500 with eight time points. To decide if there is enough power researchers should inspect their data, hypothesize about effect sizes and consider an appropriate model before applying an ITS design to their research. This paper contributes to the field of methodology in two ways. Firstly, the motivation example showcases the difficulty of employing ITS designs in cases which do not adhere to a single intervention. Secondly, models are proposed for more difficult ITS designs and their performance is tested.

PubMed Disclaimer

Conflict of interest statement

The authors have declared that no competing interests exist.

Figures

Fig 1
Fig 1. Individual growth curves for 25 students per cohort sampled randomly from CITO data.
The grey area represents the lockdown periods.
Fig 2
Fig 2. The simulation situations.
The dashed line indicates the first intervention and the dotted line the second intervention.
Fig 3
Fig 3. Power of the step for simulation scenario with a step and slope change.
Fig 4
Fig 4. Power of the slope for simulation scenario with a step and slope change.
Fig 5
Fig 5. Absolute bias of the step for simulation scenario with a step and slope change and an additional step change.
Fig 6
Fig 6. Absolute bias of the slope for simulation scenario with a step and slope change and an additional step change.
Fig 7
Fig 7. Power of the step for simulation scenario with a step change, a slope change and an additional step change with correction.
Fig 8
Fig 8. Power of the slope for simulation scenario with a step change, a slope change and an additional step change with correction.
Fig 9
Fig 9. Power of the additional step for simulation scenario with a step change, a slope change and an additional step change with correction.
Fig 10
Fig 10. Power of the step for simulation scenario with a step change, a slope change and a correction for changing slope.
Fig 11
Fig 11. Power of the slope for simulation scenario with a step change, a slope change and a correction for a changing slope.
See this image and copyright information in PMC

References

    1. Akobeng Al K. Understanding randomised controlled trials. Archives of disease in childhood. 2005;90(8):840–844. BMJ Publishing Group Ltd. doi: 10.1136/adc.2004.058222 - DOI - PMC - PubMed
    1. Porta Miquel. A dictionary of epidemiology. Oxford university press. 2014.
    1. Craig Peter, Cooper Cyrus, Gunnell David, Haw Sally, Lawson Kenny, Macintyre Sally, et al.. Using natural experiments to evaluate population health interventions: new Medical Research Council guidance. J Epidemiol Community Health. 2012;66(12):1182–1186. doi: 10.1136/jech-2011-200375 - DOI - PMC - PubMed
    1. Engzell Per, Frey Arun, Verhagen Mark D. Learning loss due to school closures during the COVID-19 pandemic. Proceedings of the National Academy of Sciences. 2021;118(17):e2022376118. doi: 10.1073/pnas.2022376118 - DOI - PMC - PubMed
    1. Cawley John, Meyerhoefer Chad, Newhouse David. The impact of state physical education requirements on youth physical activity and overweight. Health economics. 2007;16(12):1287–1301. Wiley Online Library. doi: 10.1002/hec.1218 - DOI - PubMed