A topological Hund nodal line antiferromagnet

Abstract

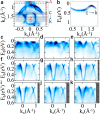
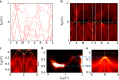
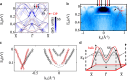
The interplay of topology, magnetism, and correlations gives rise to intriguing phases of matter. In this study, through state-of-the-art angle-resolved photoemission spectroscopy, density functional theory, and dynamical mean-field theory calculations, we visualize a fourfold degenerate Dirac nodal line at the boundary of the bulk Brillouin zone in the antiferromagnet YMn₂Ge₂. We further demonstrate that this gapless, antiferromagnetic Dirac nodal line is enforced by the combination of magnetism, space-time inversion symmetry, and nonsymmorphic lattice symmetry. The corresponding drumhead surface states traverse the whole surface Brillouin zone. YMn₂Ge₂ thus serves as a platform to exhibit the interplay of multiple degenerate nodal physics and antiferromagnetism. Interestingly, the magnetic nodal line displays a d-orbital dependent renormalization along its trajectory in momentum space, thereby manifesting Hund's coupling. Our findings offer insights into the effect of electronic correlations on magnetic Dirac nodal lines, leading to an antiferromagnetic Hund nodal line.

Fig. 1. Fermi surface and AFM Dirac line in YMn₂Ge₂.

a The crystal structure of YMn₂Ge₂. The purple arrows indicate that the two adjacent ferromagnetic Mn layers have opposite spin directions. b Bulk and surface Brillouin zones (BZs) of YMn₂Ge₂. High symmetry points are marked. The magnetic nodal line around the boundary of the BZ is highlighted by the green line. c ARPES Fermi surface spectrum on the (001) surface. The black square represents the surface BZ. Red dashed lines indicate ARPES dispersion cuts 1–3 in (e–j). d Calculated Fermi surface map corresponding to the black box in c and integrated over all the k_z values. The same plot is also embedded in c. ARPES dispersion map (e), and the corresponding bulk band structure calculation (f) along cut 1 in (c). SS stands for surface state. High symmetry points are marked. Mn $d_{z^2}$ (blue) and $d_{\mathrm{xy}}$ (red) orbitals are projected on the bulk bands. The Fermi level in (f) is adjusted according to the experimental data and DFT is renormalized by 3. Two doubly degenerate bands cross at the A point to form a fourfold degeneracy. Thick red dashed line shows that the binding energy of the Dirac crossing at the A point in the renormalized DFT differs from experimental data. ARPES dispersion map (g), and the corresponding bulk band structure calculation (h) along cut 2 in (c). A fourfold Dirac crossing can be seen at the R point. The thick red dashed line shows the consistency between the renormalized DFT and experimental data especially at the R point. ARPES dispersion map (i), and the corresponding bulk band structure calculation (j) along cut 3 in (c). Thick red dashed lines suggest that although the renormalized DFT correctly describes the band dispersion near the R point, it doesn’t agree well with ARPES data at the A point. Black arrow in (j) indicates the nodal line, and A and R points consist of mostly $d_{z^2}$ and $d_{xy}$ orbitals, respectively.

Fig. 2. Detailed characterization of the AFM nodal line.

a ARPES Fermi surface spectrum on the (001) surface in the second Brillouin zone. The black dotted box represents the second Brillouin zone and corresponding high symmetry points are marked. Red dashed line on the boundary of the Brillouin zone indicates the dispersion map in (b). Nine black lines represent the dispersion maps from (c–k). b ARPES dispersion map along the A-R-A high symmetry direction. Red cross signs are the extracted energy and momentum positions of the Dirac crossings in (c–k). c–k Corresponding ARPES dispersion maps demonstrating the fourfold degenerate crossings along the AFM nodal line. The grey-shaded areas in (h–k) mask the distorted spectra at large angles of the ARPES analyzer.

Fig. 3. YMn₂Ge₂ as a topological Hund metal.

a DFT calculation of the bulk electronic structure in YMn₂Ge₂ with spin-orbit coupling and magnetism included. b DFT + DMFT calculation of the bulk electronic structure in YMn₂Ge₂. A clear renormalization of the bands near the Fermi level can be resolved compared with (a). c DFT + DMFT electronic band structure along A-Z-A direction. The black circle indicates the location of the nodal point. d, Experimental AFM nodal line along A-R direction (same as Fig. 1i). e DFT + DMFT band structure showing an excellent agreement with (d). The two blue dashed lines confirm the consistency of DFT + DMFT and ARPES data, especially at the R and A points.

Fig. 4. Drumhead surface state associated with the AFM nodal line.

a Semi-infinite surface calculations along the $\overline{\mathrm{X}}$-$\overline{\mathrm{\Gamma }}$-$\overline{\mathrm{X}}$ high symmetry direction. Color bar shows the surface state contribution. Red dashed lines are the bulk states on the A-R-Z plane. Black and red arrows represent the drumhead surface states associated with the AFM nodal line and the bulk state on the A-R-Z plane, respectively. Black dashed line marks the experimental Fermi level. SS and DP mean surface state and Dirac point, respectively. b ARPES dispersion map along the R-Z-R high symmetry direction. A high-resolution dispersion map (same as cut 2 in Fig. 1) at the center of the Brillouin zone (Z point) is embedded to highlight the surface and bulk states. Red and black dashed lines demonstrate the bulk Dirac crossing and the drumhead surface state at R point, respectively. Red arrows are the bulk states in (a) and black arrows represent the drumhead surface state also marked in (a). c Extracted dispersions of the bulk (red dots) and drumhead surface states (black dots) near the Fermi level. Error bars correspond to the experimental momentum and energy resolutions. Black dashed lines are the linear (left) and quadratic (right) fits to the ARPES data. d Illustration of the energy dispersion of the drumhead surface states near the Fermi level.