Renormalization of radiobiological response functions by energy loss fluctuations and complexities in chromosome aberration induction: deactivation theory for proton therapy from cells to tumor control

Abstract

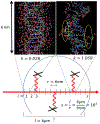
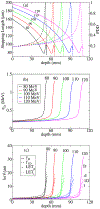
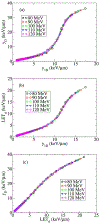
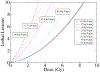
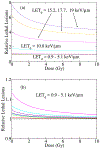
We employ a multi-scale mechanistic approach built upon our recent phenomenological/computational methodologies [R. Abolfath et al., Sci. Rep. 7, 8340 (2017)] to investigate radiation induced cell toxicities and deactivation mechanisms as a function of linear energy transfer in hadron therapy. Our theoretical model consists of a system of Markov chains in microscopic and macroscopic spatio-temporal landscapes, i.e., stochastic birth-death processes of cells in millimeter-scale colonies that incorporates a coarse-grained driving force to account for microscopic radiation induced damage. The coupling, hence the driving force in this process, stems from a nano-meter scale radiation induced DNA damage that incorporates the enzymatic end-joining repair and mis-repair mechanisms. We use this model for global fitting of the high-throughput and high accuracy clonogenic cell-survival data acquired under exposure of the therapeutic scanned proton beams, the experimental design that considers γ-H2AX as the biological endpoint and exhibits maximum observed achievable dose and LET, beyond which the majority of the cells undergo collective biological deactivation processes. An estimate to optimal dose and LET calculated from tumor control probability by extension to ~10⁶ cells per mm-size voxels is presented. We attribute the increase in degree of complexity in chromosome aberration to variabilities in the observed biological responses as the beam linear energy transfer (LET) increases, and verify consistency of the predicted cell death probability with the in vitro cell survival assay of approximately 100 non-small cell lung cancer (NSCLC) cells. The present model provides an interesting interpretation to variabilities in α and β indices via perturbative expansion of the cell survival fraction (SF) in terms of specific and lineal energies, z and y, corresponding to continuous transitions in pair-wise to ternary, quaternary and more complex recombination of broken chromosomes from the entrance to the end of the range of proton beam.

Fig. 1.

Schematically shown the partitioning of a cell nucleus (circular structure) into segments of proton-tracks (red lines) used as unit of ionization per MD simulation of DNA damage. The model calculation starts with scoring the ionizations and the time-evolution of chemical reactivity of species induced by ionized water molecules, in surrounding of DNA in sub nanometer and femto-second spatiotemporal scales. In upper left corner, a magnified structure of DNA surrounded by water molecules is depicted with no scored DSB induction. Shown in upper right corner, a typical snap-shot of distorted DNA obtained after running MD for ≈50ps. Two SSBs are highlighted by yellow circles, located within 10 base-pairs separation are indication of a DSB formation. Damaged bases, distorted hydrogen bonds, base-stacking as well as complex species such as hydrogen-peroxides formed from two OH^• free radicals are visible. For clarity of the visualization, we removed water molecules from the image of the DNA molecule.

Fig. 2.

(a) Schematic diagram of Markov process in DSB rate equation, equation (1). (b) Schematic representation of DSB induction in a cell nucleus. The bold arrow represent a charged particle traversing cell nucleus. The wiggly lines were adopted from Feynman’s diagrams in quantum electrodynamics (QED) to describe propagation of interaction of a particle as a field in scattering processes with an interaction-site (see for example Ref. [52]). (c) Chromosomes undergo DSB induction after track of particles traverse the cell. Colored lines represent chromosomes and the gap between each chromosome represent a DSB. The black dots in the middle of each chromosome represent centromere. Black chromosomes were not gone through DSB formation after traversing charged particles.

Fig. 3.

Diagrammatic representation of cell survival in form of a perturbative expansion described by pair-wise, ternary, quaternary, and N-tuple chromosome end-joining corresponding to γ₂, γ₃, γ₄ and γ_N equation (3). Possible combinations of lethal misrepaired lesions are sketched.

Fig. 4.

Shown (a) $\overline{l}$ and energy deposition percentage depth dose normalized to its value at the Bragg peak (PDD) (b) energy deposition modeled in SF, ${\epsilon }_D=\overline{{\epsilon }^2}/\overline{\epsilon }$ and (c) four types of LET averaging used in this work vs. depth for pencil beams of protons with nominal energies, 80, 90, 100, 110, and 120 MeV. The letters D,d,t and 1D, denote lineal-energy averaged LET, $y_D=\overline{y^2}/\overline{y}$, dose-averaged LET, LET_d, and two types of track-averaged LETs, ${\mathrm{LET}}_t=\overline{\epsilon }/\overline{l}$ and $y_{1D}={\epsilon }_D/\overline{l}$ respectively.

Fig. 5.

Shown (a) y_D (or LET_y) vs. y_1D, (b) LET_d vs. y_1D and (c) y_D vs. LET_d calculated by Geant MC toolkit. The simulation consists of 10⁶ particles in water phantom. A universal linear relation in low LET less than 5 keV/μm is visible. As LET increases a non-linear dependence emerges and the lines show slightly divergence because of energy loss straggling in the end of proton range.

Fig. 6.

Shown H460 and H1437 cell survival as a function of dose (Gy) and dose averaged LET_d (keV/μm). The blue dots are the result of 3D surface fitting to the experimental data presented in reference [41] with a gap between low and high LETs, 5.08 ≤ LET_d ≤ 10.8. This gap appears because of lack of experimental data in intermediate domain of LET’s. In low and high LETs two sets of linear and non-linear polynomials used. The fitted surfaces to the blue dots are the result of second/post-processing fitting procedure presented in this work that provides a continuous and smooth connection between low and high LET data sets within intermediate domain of LETs.

Fig. 7.

Shown H460 lethal lesions per cell as a function of dose and LETs. The lethal lesions calculated using linear-quadratic model $\overline{L}=\alpha D+\beta D^2$. The labels over each line represent experimental values of LET for specific lethal lesion curve.

Fig. 8.

Shown H460 (a and b) relative lethal lesions per cell as a function of dose for different LETs. The relative lethal lesions, $\overline{L}\left({\mathrm{LET}}_d\right)/\overline{L}({\mathrm{LET}}_d=0.9)$, were calculated using 3D global fitting of the experimental cell survival data within LQ model. It represents $\overline{L}\left({\mathrm{LET}}_d\right)$, normalized by the lethal lesions at the lowest LET, $\overline{L}({\mathrm{LET}}_d=0.9)$. For a better visualization of relative lethal lesions in low LETs, a magnified version of (a) is shown in (b).

Fig. 9.

Shown the tumor control probability, TCP, of 10⁶ H460 NSCLC in a typical mm-size volume. As the number of cells in the volume increases the sigmoid curve shifts to higher doses.

Fig. 10.

Shown (a) experimental (circles) fitted by three-dimensional global fitting (red bold lines) of cell survival fraction (SF) and (b) the cell death probability (CDP) of 100 H460 NSCLC used experimentally to measure SF in a 12 wells-plate as a function of dose and LET, irradiated by a single fraction of scanning proton with approximate nominal energy of 80MeV. The end points in SF where the radiation dose is highest, are indicated by arrows in (a), coincide with the onset of CDP sigmoid turning points. A sharp rise in sigmoid justifies termination in viability of cells seeded in the well, hence, a drop in their biological responses. With increase in LET, the maximum experimentally achievable doses in cell viability that terminate SF curves, lowers.