Superlubric Graphullerene

Abstract

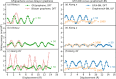
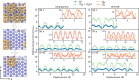
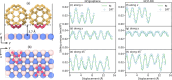
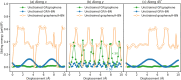
Graphullerene (GF), an extended quasi-two-dimensional network of C₆₀ molecules, is proposed as a multicontact platform for constructing superlubric interfaces with layered materials. Such interfaces are predicted to present very small and comparable sliding energy corrugation regardless of the identity of the underlying flat layered material surface. It is shown that, beyond the geometrical effect, covalent interlinking between the C₆₀ molecules results in reduction of the sliding energy barrier. For extended GF supercells, negligible sliding energy barriers are found along all sliding directions considered, even when compared to the case of the robust superlubric graphene/h-BN heterojunction. This suggests that multicontact architectures can be used to design ultrasuperlubric interfaces, where superlubricity may persist under extreme sliding conditions.

Keywords: density functional theory calculations; graphullerene; interlayer potentials; multicontact; registry index; sliding energy corrugation; structural superlubricity.

Figure 1

Heterojunction model system. (a) Top view of the rectangular GF (1 × 1)/h-BN (2 × 6) supercell containing 120 carbon (yellow spheres), 24 nitrogen (blue spheres), and 24 boron (pink spheres) atoms. (b) Binding energy curves of GF/graphene (filled blue circles), GF/h-BN (filled orange circles), graphene (empty blue circles), and graphene/h-BN (empty orange circles) bilayers. The inset shows the definition of the interlayer distance, d, as the vertical distance between the lowest GF atom and the plane of the flat substrate. Also shown is the distance between adjacent contact points, L, which is larger than the lattice vector of the underlying flat layer, l (L > l), thus forming a multicontact interface. The OVITO package was used for visualizing atomic structures.

Figure 2

Sliding energy profiles of vertically flexible (a–c) GF/graphene (filled green circles) and bilayer graphene (empty red circles) and (d–f) GF/h-BN (filled blue circles) and graphene/h-BN (empty orange circles), calculated along the x (armchair, top), y (zigzag, middle), and in-plane 45° (bottom) sliding directions. For the graphene/h-BN interface, 52 × 52 graphene supercells and 51 × 51 h-BN supercells were used to ensure that the lattice strain in both layers does not exceed 0.1%. Due to the large supercell size, DFT calculations were not feasible in this case; hence, we performed the calculations using a dedicated classical interlayer potential (ILP) that reproduces well the DFT results. For the sake of clarity, the DFT results of the GF/graphene and GF/h-BN systems are multiplied by 50 and the ILP results for the graphene/h-BN interface are multiplied by 1000. For graphene/h-BN, a sliding length of 10 Å was used for all three directions. For all other bilayers, along the x and y directions, a sliding length equal to the lattice constant was used to maintain periodicity, whereas for sliding along the in-plane 45° direction, a sliding length of 14 Å was selected. All results are presented relative to the corresponding minimum energy point along each sliding profile.

Figure 3

Evidence for chemical effects on friction. (a–c) Schematic representation of the individual C₆₀ molecules (C₆₀^a (panel b) and C₆₀^b (panel c)) cut out of the GF layer (a). (d–f) Sliding energy curves (normalized per buckyball) of the two individual C₆₀ molecules (empty orange and red triangles in the insets) and their sum (empty green circles) sliding on graphene, compared to the GF sliding profile (filled blue circles). (g–l) Same as panels d–f but for an h-BN substrate. Sliding paths along different substrate lattice directions are considered, including (d and g) the armchair (x) direction, (e and h) the zigzag (y) direction, and (f and l) 45° between them. All results are presented relative to the corresponding minimum energy point along each sliding profile.

Figure 4

RI calculations. (a) Front and (b) top schematic views of the GF surface contacting atoms (colored red). For the RI calculations, all GF atoms residing within a vertical distance of 3.7 Å from the underlying graphene or h-BN surface are considered to be in direct contact with the substrate.^, Vertically flexible sliding energy profiles of (c–e) GF/graphene and (f–h) GF/h-BN calculated using DFT (empty blue circles) are compared to the scaled RI results (solid green lines). The DFT results are vertically shifted, such that the total energy of the lowest interlayer energy configuration of all three sliding directions considered is set as the origin. Sliding paths along different substrate lattice directions are considered, including (c and f) the armchair (x) direction, (d and g) the zigzag (y) direction, and (e and h) 45° between them. Scaling of the RI results is performed by multiplying the RI profile by a constant factor (0.0387 meV/Ų for GF/graphene and 0.0400 meV/Ų for GF/h-BN) to obtain good agreement with the DFT results.

Figure 5

Scaled rigid sliding RI profiles of unstrained GF (7 × 7)/graphene (15 × 45) (filled green circles) and GF (10 × 13)/h-BN (21 × 82) (filled blue circles) interfaces, compared to unstrained graphene (52 × 52)/h-BN (51 × 51) vertically flexible ILP sliding energy profiles (empty orange circles). Sliding paths along different substrate lattice directions are considered, including (a) the armchair (x) direction, (b) the zigzag (y) direction, and (c) 45° between them. All results are presented relative to the corresponding minimum energy point along each profile. For the sake of clarity, the results for unstrained GF/h-BN and GF/graphene along the y-axis are multiplied by 50.