Bounding the Softwired Parsimony Score of a Phylogenetic Network

Abstract

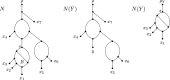
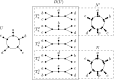
In comparison to phylogenetic trees, phylogenetic networks are more suitable to represent complex evolutionary histories of species whose past includes reticulation such as hybridisation or lateral gene transfer. However, the reconstruction of phylogenetic networks remains challenging and computationally expensive due to their intricate structural properties. For example, the small parsimony problem that is solvable in polynomial time for phylogenetic trees, becomes NP-hard on phylogenetic networks under softwired and parental parsimony, even for a single binary character and structurally constrained networks. To calculate the parsimony score of a phylogenetic network N, these two parsimony notions consider different exponential-size sets of phylogenetic trees that can be extracted from N and infer the minimum parsimony score over all trees in the set. In this paper, we ask: What is the maximum difference between the parsimony score of any phylogenetic tree that is contained in the set of considered trees and a phylogenetic tree whose parsimony score equates to the parsimony score of N? Given a gap-free sequence alignment of multi-state characters and a rooted binary level-k phylogenetic network, we use the novel concept of an informative blob to show that this difference is bounded by $k+1$ times the softwired parsimony score of N. In particular, the difference is independent of the alignment length and the number of character states. We show that an analogous bound can be obtained for the softwired parsimony score of semi-directed networks, while under parental parsimony on the other hand, such a bound does not hold.

Keywords: Level-k; Parental parsimony; Phylogenetic networks; Softwired parsimony.

Fig. 1

A phylogenetic network N (left), an embedding S of a phylogenetic X-tree displayed by N together with a binary character f and an extension F (middle; also indicated by the dashed lines in the left panel), and the phylogenetic X-tree T obtained from S by suppressing vertices of in-degree one and out-degree one (right)

Fig. 2

An example of a blob reduction applied to a phylogenetic network N that replaces the maximal blob B with source s and $\text{cl}(s)=\{x_1,x_2,x_3\}$ with a single new leaf y to obtain $N(\overline{Y})$

Fig. 3

An embedding S of a phylogenetic X-tree that is displayed by the phylogenetic network N on X as shown in Fig. 2, the cluster tree pair $(S(Y),S(\overline{Y}))$ of S relative to the blob B that is also shown in Fig. 2, and a pair of cluster extensions $F_Y$ and $F_{\overline{Y}}$ with respect to the character f on X. For reasons of clarity, the extensions $F_Y$ and $F_{\overline{Y}}$ to the vertices of S(Y) and $S(\overline{Y})$, respectively, are only shown for some vertices. Observe that $F_{\overline{Y}}(y)=F_Y({\rho }_Y)$ and that all leaves of S(Y) and $S(\overline{Y})$, except for y, are assigned to the same character state as in S

Fig. 4

A level-k network N on $X=\{x_0\}\cup \{x_i,x_i^{\prime },x_i^{\prime \prime }:1\le i\le k\}$ (left) and two phylogenetic X-trees T and $T^{\prime }$ displayed by N together with a binary character f and extensions F and $F^{\prime }$ to V(T) and $V(T^{\prime })$, respectively (right)

Fig. 5

A phylogenetic network N on $X=\{x_1,x_2,\dots ,x_4\}$, a phylogenetic X-tree T such that $T\in P(N)$ and $T\notin D(N)$, and the multilabelled tree $U^{\ast }(N)$. The dashed lines in N indicate how T can be drawn inside N

Fig. 6

A level-1 network N on $X=\{x_1,x_2,\dots ,x_{n+1}\}$ with n being even and two parental trees T and $T^{\prime }$ of N together with a binary character f on X. Here, $P{S}_{\text{pa}}(N,f)=PS(f,T^{\prime })=1$, whereas $PS(f,T)=n/2$

Fig. 7

An unrooted level-1 network U (left) with its display set D(U) (middle), and two orientations N and $N^{\prime }$ of U (right) with their respective display sets indicated by a dashed rectangle. More precisely, D(N) and $D(N^{\prime })$ can be obtained by orienting the enclosed unrooted phylogenetic X-trees