Sequence-encoded Spatiotemporal Dependence of Viscoelasticity of Protein Condensates Using Computational Microrheology

Abstract

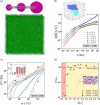
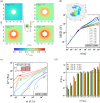
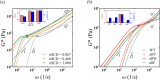
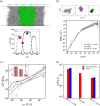
Many biomolecular condensates act as viscoelastic complex fluids with distinct cellular functions. Deciphering the viscoelastic behavior of biomolecular condensates can provide insights into their spatiotemporal organization and physiological roles within cells. Though there is significant interest in defining the role of condensate dynamics and rheology in physiological functions, the quantification of their time-dependent viscoelastic properties is limited and mostly done through experimental rheological methods. Here, we demonstrate that a computational passive probe microrheology technique, coupled with continuum mechanics, can accurately characterize the linear viscoelasticity of condensates formed by intrinsically disordered proteins (IDPs). Using a transferable coarse-grained protein model, we first provide a physical basis for choosing optimal values that define the attributes of the probe particle, namely its size and interaction strength with the residues in an IDP chain. We show that the technique captures the sequence-dependent viscoelasticity of heteropolymeric IDPs that differ either in sequence charge patterning or sequence hydrophobicity. We also illustrate the technique's potential in quantifying the spatial dependence of viscoelasticity in heterogeneous IDP condensates. The computational microrheology technique has important implications for investigating the time-dependent rheology of complex biomolecular architectures, resulting in the sequence-rheology-function relationship for condensates.

Fig. 1.

(a) Simulation snapshot of the dense phase of a condensate formed by a select E–K sequence (nSCD = 1) of chain length $N=250$ with a spherical probe particle (magenta) of hydrodynamic radius $R_{\mathrm{h}}$ embedded in it. (b) Mean square displacement $\mathrm{M}\mathrm{S}\mathrm{D}(t)$ of the center of mass of the probe particle for different $R_{\mathrm{h}}$ in the dense phase of the E–K sequence with nSCD = 1. The dashed lines are the fits based on the Baumgaertel-Schausberger-Winter-like power law spectrum to the MSD data. The inset shows probe’s displacement in the three-dimensional Cartesian coordinates for select $R_{\mathrm{h}}$ values. (c) Elastic $G^{\prime }$ (dashed line) and viscous $G^{\prime \prime }$ (solid line) modulus for the dense phase of the E–K sequence with nSCD = 1 as a function of $R_{\mathrm{h}}$, with circles corresponding to the crossover frequency. The inset shows the relaxation time $\tau$, computed as the inverse of crossover frequency, with varying $R_{\mathrm{h}}$. (d) Viscosity $\eta$, normalized by that obtained based on the Green-Kubo (GK) relation ${\eta }_{\mathrm{G}\mathrm{K}}$, as a function of normalized probe particle size $R_{\mathrm{h}}/\xi$, where $\xi$ is the correlation length, for three different nSCD sequences. The two shaded regions delineate regions where $R_{\mathrm{h}}$ is smaller or larger than $\xi$. The black dashed line corresponds to $\eta ={\eta }_{\mathrm{G}\mathrm{K}}$.

Fig. 2.

(a) Velocity $v_x$ profile of the residues of protein chains with nSCD = 1 around the probe particle translating with a velocity $v_{x,\text{probe}}$ for different probe-protein interaction strengths $\epsilon$, normalized by the strongest possible interaction strength $\epsilon =0.20\mathrm{k}\mathrm{c}\mathrm{a}\mathrm{l}/\mathrm{m}\mathrm{o}\mathrm{l}$ in the HPS model. (b) Mean square displacement $\mathrm{M}\mathrm{S}\mathrm{D}(t)$ of the center of mass of the probe particle for different $\epsilon /{\epsilon }_{\mathrm{H}\mathrm{P}\mathrm{S}}$ in the dense phase of the E–K sequence with nSCD = 1. The dashed lines are the fits based on Baumgaertel-Schausberger-Winter-like power law spectrum to the MSD data. The inset shows probe’s displacement in the three-dimensional Cartesian coordinates for select $\epsilon /{\epsilon }_{\text{HPS}}$ values. (c) Elastic $G^{\prime }$ (dashed line) and viscous $G^{\prime \prime }$ (solid line) modulus for the dense phase of the E–K sequence with nSCD = 1 as a function of $\epsilon /{\epsilon }_{\mathrm{H}\mathrm{P}\mathrm{S}}$, with circles corresponding to the crossover frequency. The inset shows the relaxation time $\tau$ with varying $\epsilon /{\epsilon }_{\mathrm{H}\mathrm{P}\mathrm{S}}$. (d) Viscosity $\eta$, normalized by that obtained based on the Green-Kubo (GK) relation ${\eta }_{\mathrm{G}\mathrm{K}}$ as a function of $\epsilon /{\epsilon }_{\mathrm{H}\mathrm{P}\mathrm{S}}$ for three different nSCD sequences. The black dashed line corresponds to $\eta ={\eta }_{\mathrm{G}\mathrm{K}}$.

Fig. 3.

(a) Elastic $G^{\prime }$ (dashed line) and viscous $G^{\prime \prime }$ (solid line) modulus for three E–K sequences with different nSCD, obtained based on multiple $\left(n=8\right.)$ probes in each dense phase system. (b) Elastic $G^{\prime }$ (dashed line) and viscous $G^{\prime \prime }$ (solid line) modulus for A1-LCD WT and its three variants, obtained based on multiple $(n=6)$ probes in each dense phase system. The circles in (a) and (b) correspond to the sequence-specific crossover frequencies. The insets in (a) and (b) shows the changes in relaxation time $\tau$ and viscosity $\eta$ with changing nSCD and with mutational changes in the A1-LCD WT sequence, respectively.

Fig. 4.

(a) Simulation snapshot of a heterogeneous condensate formed by two different E–K sequences with nSCD = 0.067 and nSCD = 1.000. Three probe particles are spatially restrained in three regions of the heterogeneous condensate: one among nSCD = 1.000 chains, one among nSCD = 0.067 chains, and one at the interface of the two nSCD sequences. Also shown are the density profiles of the heterogeneous condensate. (b) Mean square displacement $\mathrm{M}\mathrm{S}\mathrm{D}(t)$ of the probe particle in three different regions of the heterogeneous condensate. The dashed lines are the fits based on Baumgaertel-Schausberger-Winter-like power law spectrum to the MSD data. The inset shows probe’s displacement in the two-dimensional Cartesian coordinates in the chosen regions within the condensate. (c) Elastic $G^{\prime }$ (open symbols) and viscous $G^{\prime \prime }$ (closed symbols) modulus sampled from three different regions of the heterogeneous condensate, with circles corresponding to the location-specific crossover frequency. The inset shows the relaxation time $\tau$ in the chosen regions within the condensate. (d) Viscosity $\eta$ in three regions of the heterogeneous condensate compared with those obtained from the bulk simulations of the E–K sequences.