Generative Models for Periodicity Detection in Noisy Signals
- PMID: 39189192
- PMCID: PMC11348253
- DOI: 10.3390/clockssleep6030025
Generative Models for Periodicity Detection in Noisy Signals
Abstract
We present the Gaussian Mixture Periodicity Detection Algorithm (GMPDA), a novel method for detecting periodicity in the binary time series of event onsets. The GMPDA addresses the periodicity detection problem by inferring parameters of a generative model. We introduce two models, the Clock Model and the Random Walk Model, which describe distinct periodic phenomena and provide a comprehensive generative framework. The GMPDA demonstrates robust performance in test cases involving single and multiple periodicities, as well as varying noise levels. Additionally, we evaluate the GMPDA on real-world data from recorded leg movements during sleep, where it successfully identifies expected periodicities despite high noise levels. The primary contributions of this paper include the development of two new models for generating periodic event behavior and the GMPDA, which exhibits high accuracy in detecting multiple periodicities even in noisy environments.
Keywords: algorithm; generative models; periodic leg movements during sleep; periodicity; periodicity detection.
Conflict of interest statement
The authors declare no conflicts of interest.
Figures










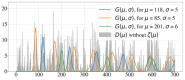


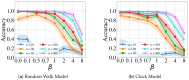





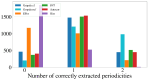
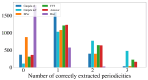





References
-
- Welch P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967;15:70–73. doi: 10.1109/TAU.1967.1161901. - DOI
-
- Priestley M.B. Spectral Analysis and Time Series: Univariate Series. Academic Press; London, UK: 1981.
-
- Madsen H. Time Series Analysis. CRC Press; Boca Raton, FL, USA: 2007.
-
- Mitsa T. Temporal Data Mining. CRC Press; Boca Raton, FL, USA: 2010.
-
- Box G.E.P., Jenkins G.M., Reinsel G.C., Ljung G.M. Time Series Analysis: Forecasting and Control. John Wiley & Sons; New York, NY, USA: 2015.
Grants and funding
LinkOut - more resources
Full Text Sources

