Contrast Information Dynamics: A Novel Information Measure for Cognitive Modelling

Abstract

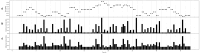
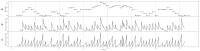
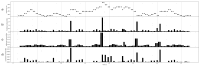
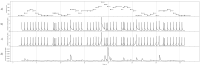
We present contrast information, a novel application of some specific cases of relative entropy, designed to be useful for the cognitive modelling of the sequential perception of continuous signals. We explain the relevance of entropy in the cognitive modelling of sequential phenomena such as music and language. Then, as a first step to demonstrating the utility of constrast information for this purpose, we empirically show that its discrete case correlates well with existing successful cognitive models in the literature. We explain some interesting properties of constrast information. Finally, we propose future work toward a cognitive architecture that uses it.

Keywords: Gaussian process; Markov process; cognitive modelling; continuous systems; coordinate invariance; information dynamics; information measure; information theory; predictive information; specific information.

Figure 1

An example of the contrast information associated with a discrete-time, discrete-state stochastic process. In (a), a MIDI representation of a folk melody is represented as a discrete-time process through a uniform sampling in time of the data. The discrete state space of the process is inhabited by the MIDI pitch numbers. Note that, though the visualisation represents the pitches as an ordered set, we treat the pitches as an unordered set of discrete states. Through treating all melodies in the corpus as instances of the same stationary first-order DTMC, the maximum likelihood estimate of the transition matrix of the DTMC was found. In (b,c), the forward predictive contrast information profile and forward reflective contrast information profile are shown for the melody in (a), calculated using the estimated DTMC. Each bar is centred on the present Y, where the past X is the immediately previous pitch, and the future Z is the immediately next pitch. The connective contrast information is omitted here since it is always zero for Markov processes.

Figure 2

An example of the contrast information associated with a continuous-time, discrete-state stochastic process. In (a), a MIDI representation of a folk melody is represented as a continuous-time process, where the onset of a state is indicated by a triangle, and the duration of a state is indicated by the horizontal line. The discrete state space of the process is inhabited by the MIDI pitch numbers. Note that, though the visualization represents the pitches as an ordered set, we treat the pitches as an unordered set of discrete states. Through treating all melodies in the corpus as instances of the same stationary CTMC, the maximum likelihood estimate of the rate matrix of the CTMC was found. In (b), the forward predictive contrast information profile is shown. The present Y is located at the most recent pitch onset, and the past X is located at the pitch onset immediately before Y. Each point on the profile curve is centred on the future Z, which varies in time from the most recent pitch onset (Y) to the next pitch onset, at which point the past and present shift forward to the next pitch onsets. In (c), the forward reflective contrast information profile is shown. The past X is located at the most recent pitch onset. The future Z is located at the next pitch onset. Each point in the profile curve is centred on the present Y, which varies in time from the most recent pitch X to next pitch Z, at which point, the past and future shift forward to the next pitch onsets. The connective contrast information is omitted here since it is always zero for Markov processes.

Figure 3

An example of the contrast information associated with a discrete-time, continuous-state stochastic process. In (a), a MIDI representation of a folk melody is represented as a discrete-time process through a uniform sampling in time of the data. The continuous state space of the process is inhabited by the frequencies associated with each MIDI pitch. Through treating all melodies in the corpus as instances of the same stationary Gaussian process, the maximum likelihood estimates for the mean and autocovariance of the Gaussian process were found. In (b–d), the contrast information profiles are calculated using the estimated DTGP. Each bar is centred on the present Y, where the past X is the immediately previous pitch, and the future Z is the immediately next pitch. In this case, using longer duration regimes for the past and future resulted in very similar profiles, so the profiles shown here are generally representative. Note that the scale of the connective contrast is much lower than the other predictive and reflective contrast.

Figure 4

An example of the contrast information associated with a continuous-time, continuous-state stochastic process. In (a), a MIDI representation of a folk melody is represented as a continuous-time process, where the onset of a state is indicated by a triangle, and the duration of a state is indicated by the horizontal line. The continuous state space of the process is inhabited by the frequencies associated with each MIDI pitch. Through treating all melodies in the corpus as instances of the same stationary Gaussian process, the maximum likelihood estimates for the mean and autocovariance of the discrete-time Gaussian process were found. The discrete-time autocovariance function was then fit with a high degree polynomial to obtain a continuous-time autocovariance function. In (b), the forward predictive contrast information profile is shown. The present Y is located at the most recent pitch onset, and the past X is located at the pitch onset immediate before Y. Each point on the profile curve is centred on the future Z, which varies in time from the most recent pitch onset (Y) to the next pitch onset, at which point, the past and present shift forward to the next pitch onsets. In (c), the forward reflective contrast information profile is shown. The past X is located at the most recent pitch onset. The future Z is located at the next pitch onset. Each point in the profile curve is centred on the present Y, which varies in time from the most recent pitch X to the next pitch Z, at which point, the past and future shift forward to the next pitch onsets. In (d), the forward connective contrast information profile is shown. The past, present, and future follow the same scheme as described for forward predictive contrast information in (b). Note that the scale of the connective contrast is much lower than the other the predictive and reflective contrast.